Lecture 2: Tools of the Trade

Math + Cosmic Scales Survival Kit

Dr. Anna Rosen

January 23, 2026

Learning Objectives

By the end of this lecture, you will be able to:

• Read and calculate with scientific notation (powers of ten)
• Use SI prefixes (kilo-, mega-, micro-, …) to translate scale
• Set up unit conversions so units cancel (factor-label method)
• Use the ratio method to compare planets/stars without big-number pain
• Solve simple rate problems (distance = speed × time; amount = rate × time)
• Use the astronomy “distance ladder” units: AU, light-year, parsec

Set the tone: “This is not a math test. It’s a navigation toolkit for the universe.”

A Word Before We Begin

Don’t panic about the equations!

Today I’ll show you examples using formulas we haven’t covered yet. You’re not expected to understand them fully — we’ll learn each one properly when its topic comes up.

For now, focus on the method, not the formula.

Think of it like watching a cooking demo before you have all the ingredients. You’re learning the technique — the details come later.

30 sec. This is important framing. Students often freeze when they see unfamiliar equations. Reassure them: today is about building comfort with the tools, not mastering every formula.

If the Sun were a cantaloupe in San Francisco…

…Earth would be a pinhead 15 meters away.

The nearest star? Another cantaloupe in Hawaii.

0–1 min. Pause after the first line. Let them picture it. Then reveal the fragments. This establishes why we need powers of ten — ordinary language can’t hold these scales.

Why we’re doing this

Math as a telescope 🔭

In ASTR 101, numbers aren’t decoration — they’re how we turn points of light into physical reality.

• Units keep your equations honest.
• Ratios cancel constants and reveal relationships.
• Rates connect motion, time, and change.
• Powers of ten let your brain hold the cosmos.

Today’s Toolkit

Four survival tools 🧰

1. Scientific notation + prefixes → speak “cosmic scale”
2. Units + conversions → translate cleanly
3. Ratio method → compare without drowning in zeros
4. Rate problems → connect distance, time, and speed

Cosmic Scales in One Slide

A few anchor distances (order-of-magnitude is enough today):

Scale	Distance	Light travel time
Earth–Moon	\(3.84\times10^8\,\text{m}\)	\(\sim 1.3\,\text{s}\)
1 AU (Earth–Sun)	\(1.50\times10^{11}\,\text{m}\)	\(\sim 8.3\,\text{min}\)
1 light-year (ly)	\(9.46\times10^{15}\,\text{m}\)	1 year
1 parsec (pc)	\(3.09\times10^{16}\,\text{m}\)	\(\sim 3.26\,\text{yr}\)

The key idea

Distance and time mix in astronomy because information travels at a finite speed.

We don’t see things as they are. We see them as they were.

Common trap

A light-year is a distance, not a time — even though “year” is in the name. It’s how far light travels in one year: about 9.5 trillion km.

Don’t over-precision-police here; emphasize scale literacy. You can refine numbers later.

The Speed of Light: Nature’s Speed Limit

Light is the fastest thing in the universe. Nothing can travel faster.

\[c = 300{,}000\,\text{km/s} = 3 \times 10^8\,\text{m/s}\]

• Light travels 1 meter in about 3 nanoseconds
• Light crosses Earth’s diameter in 0.04 seconds
• Light reaches the Moon in 1.3 seconds
• Light reaches the Sun in 8.3 minutes

Credit: Rubin Observatory/NSF/AURA

Every galaxy in this image is a time capsule. The light we see left millions to billions of years ago — we’re seeing them as they were, not as they are.

1.5 min. Build the speed of light from familiar to cosmic scales. Point to the Rubin Observatory deep field: “Each of these galaxies is at a different distance, so we’re seeing them at different ages. The farthest ones appear as they were billions of years ago.” This sets up the key insight: distance = looking back in time.

What a Light-Year Really Means

A light-year is a distance, not a time — even though “year” is in the name.

It’s how far light travels in one year:

\[1\,\text{ly} \approx 9.5 \times 10^{15}\,\text{m}\]

That’s about 9.5 trillion kilometers.

Why use light-years?

“Proxima Centauri is \(4 \times 10^{16}\) m away” is painful.

“4.2 light-years” is memorable.

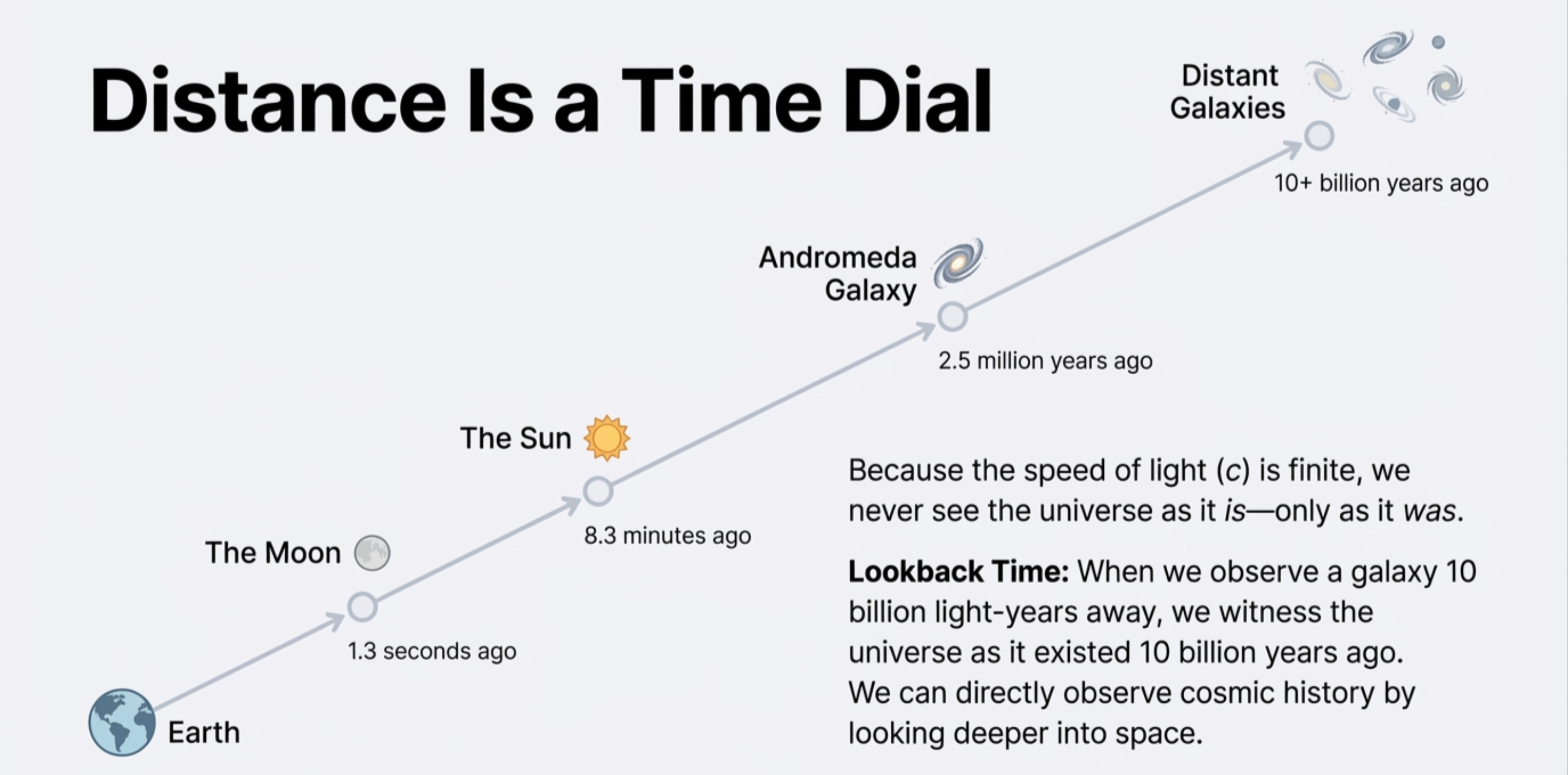
Distance Is a Time Machine

Because light takes time to travel, looking far away = looking back in time.

Object	Distance	You see it as it was…
Moon	1.3 light-sec	1.3 seconds ago
Sun	8.3 light-min	8.3 minutes ago
Proxima Centauri	4.2 ly	4.2 years ago
Andromeda Galaxy	2.5 Mly	2.5 million years ago

Mind-bending implication

The further we look, the further back in time we see.

The most distant galaxies show us the universe as it was billions of years ago.

1.5 min. Let this sink in. Distance is literally a time dial. This is why these math tools matter: we need them to decode cosmic history.

Why We Need These Tools

These cosmic scales are why we need a math survival kit:

• Scientific notation — to write \(9{,}500{,}000{,}000{,}000{,}000\) m as \(9.5 \times 10^{15}\) m
• Unit conversions — to translate between meters, km, AU, and light-years
• Ratios — to compare without drowning in zeros
• Rate problems — to connect distance, speed, and time

These aren’t abstract math exercises. They’re the tools that let us decode the universe.

1 min. This is the “why we’re doing this” slide. Connect the motivation to the tools.

The Universe’s Phone Number

Credit: Adapted from Owocki (course illustration)

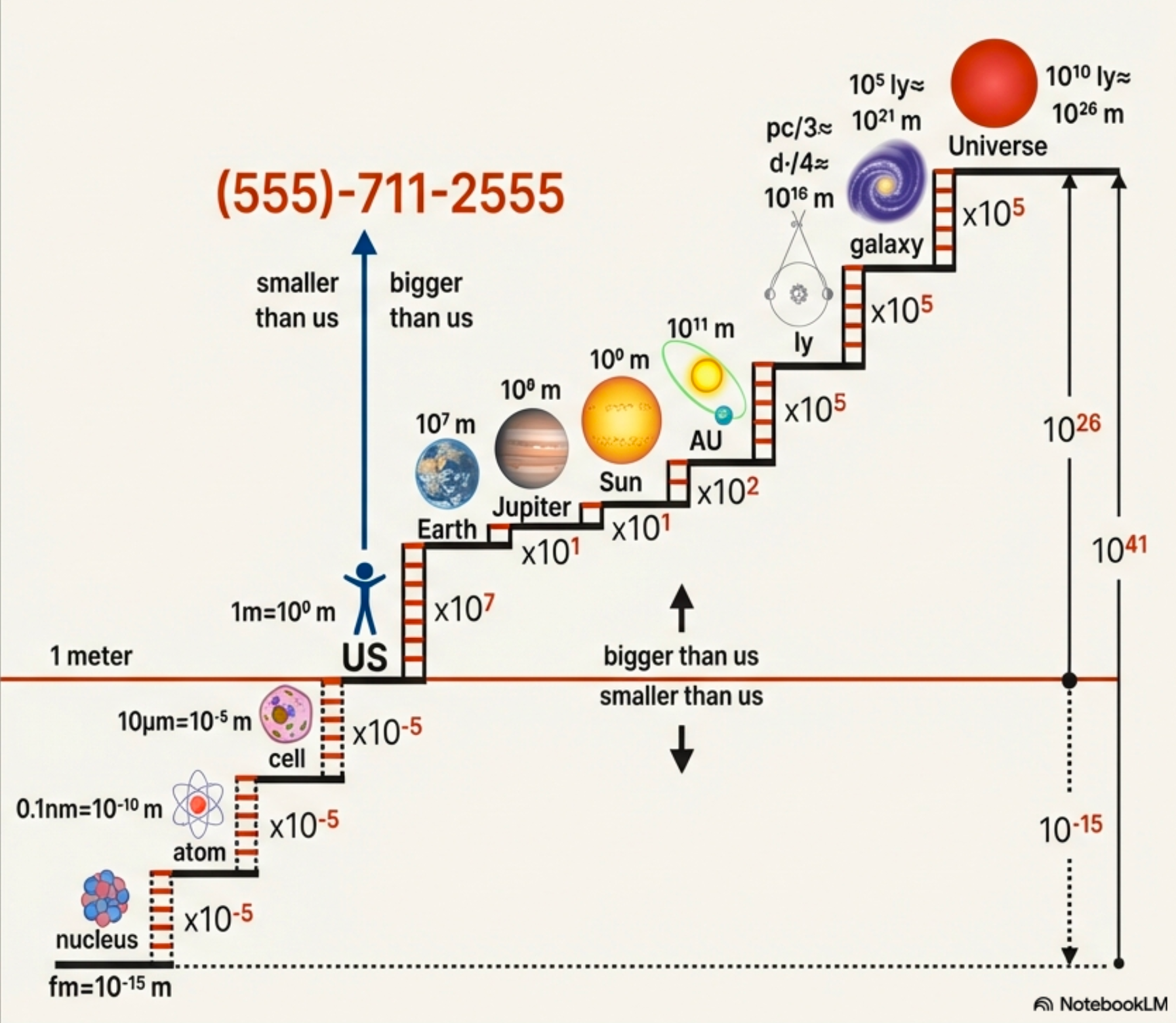
Each step on this ladder is a factor of 10.

From your desk to the edge of the observable universe takes about 27 steps.

The mnemonic

(555)-711-2555 encodes the multipliers at each scale jump. Astronomers really do use phone-number tricks to navigate cosmic scales!

1.5 min. Walk through a few steps on the ladder. Point out: human → Earth → Sun → nearest star → galaxy → observable universe. Each step is ×10, and it takes ~27 of these to span everything.

1 min. Full-screen image — let it breathe. From atoms to the observable universe, each tick is ×10. This is why we need scientific notation: ordinary numbers can’t hold 40+ orders of magnitude.

Stop & Solve 0: Light-time intuition

Light takes about 8.3 minutes to travel 1 AU.

• How long does it take light to reach us from something at 2 AU?
• How long from 0.5 AU?

→ Solution

Tool 1: Scientific Notation

Because the universe refuses to be written out in longhand

0.5 min. Section transition. Let the tagline land.

Scientific notation = brain-friendly compression

A number written as

\[a\times 10^n\]

means:

• \(a\) is the coefficient (usually between 1 and 10)
• \(10^n\) tells you how many places the decimal moves
• \(n\) is the order of magnitude (the scale)

2 min. Walk through each bullet. Have students repeat: “a is the coefficient, n is the order of magnitude.” Muscle memory matters for notation fluency.

Converting: decimal ↔︎ scientific notation

Big number

\(300{,}000{,}000\,\text{m/s} = 3.0\times10^8\,\text{m/s}\)

Small number

\(0.000000001\,\text{s} = 1.0\times10^{-9}\,\text{s}\)

Direction rule

• \(n>0\) → move decimal right (bigger)
• \(n<0\) → move decimal left (smaller)

Operations (no calculator vibe)

• Multiply: \((a\times10^m)(b\times10^n)=(ab)\times10^{m+n}\)
  • Multiply the coefficients, add the exponents
• Divide: \(\dfrac{a\times10^m}{b\times10^n}=\left(\dfrac{a}{b}\right)\times10^{m-n}\)
  • Divide the coefficients, subtract the exponents
• Powers: \((a\times10^m)^k = a^k\times10^{mk}\)
  • Raise the coefficient to the power, multiply the exponent

Why this works

Exponents are a shorthand for repeated multiplication. Adding exponents = multiplying powers of ten: \(10^3 \times 10^2 = 10^{3+2} = 10^5\).

2 min. Make them say each rule out loud once. Emphasize the pattern: coefficients do normal math, exponents follow their own rules.

Quick Check: Scientific Notation

What is \((3 \times 10^5)(4 \times 10^3)\)?

• \(7 \times 10^8\)
• \(12 \times 10^{15}\)
• \(1.2 \times 10^9\)
• \(1.2 \times 10^8\)

1-2 min. Give them 30 seconds to think. Rule: multiply coefficients, add exponents. \(3 \times 4 = 12\), \(5 + 3 = 8\), then normalize.

Answer: \(1.2 \times 10^9\)

SI Prefixes: the language of scale

Prefix	Symbol	Factor
tera	T	\(10^{12}\)
giga	G	\(10^{9}\)
mega	M	\(10^{6}\)
kilo	k	\(10^{3}\)
milli	m	\(10^{-3}\)
micro	\(\mu\)	\(10^{-6}\)
nano	n	\(10^{-9}\)

Stress: these are power-of-ten labels. They’re not extra information; they are the exponent.

Order-of-magnitude estimation (OoM)

When exact arithmetic is annoying, estimate on purpose.

• Round coefficients to nearby easy numbers.
• For a rough order-of-magnitude:
  • coefficient \(< 3\) → round to 1
  • coefficient \(> 3\) → round to 10

OoM is not “sloppy.” It’s a controlled approximation for staying in the right cosmic zip code.

Tool 2: Units & Conversions

Units are the meaning of a number

0.5 min. Section transition. Let the tagline land.

What’s a Physical Quantity?

A physical quantity = a number + a unit

✓ Physical quantities

• 3 meters
• 5.9 × 10²⁴ kg
• 300,000 km/s

✗ Not physical quantities

• “3” (three what?)
• “really far”
• “super hot”

The unit is not optional. Without it, the number is meaningless.

1 min. This seems obvious, but students often drop units mid-calculation. Emphasize: a number without a unit is like a sentence without a verb.

What’s a Physical Constant?

A physical constant is a number that nature gives us — it doesn’t change.

• Speed of light: \(c = 3 \times 10^8\) m/s — the universe’s speed limit
• Gravitational constant: \(G = 6.67 \times 10^{-11}\) m³/(kg·s²) — how strong gravity is
• Planck’s constant: \(h = 6.63 \times 10^{-34}\) J·s — the “graininess” of energy

Why do constants matter?

They’re conversion factors between different physical quantities. The speed of light \(c\) converts between distance and time. That’s why light-years work!

1.5 min. Don’t dwell on the numbers — emphasize the concept. Constants are nature’s rules, not human choices. We discover them, we don’t invent them.

Units vs. Dimensions (very light intro)

Units are human choices:

• meters vs kilometers vs AU

Dimensions are the type of quantity:

• length \([L]\), time \([T]\), mass \([M]\)

Examples:

• speed: \([L/T]\)
• area: \([L^2]\)
• volume: \([L^3]\)

Credit: (A. Rosen/NotebookLM)

Why mention dimensions?

Not to do a full “dimension analysis” unit…but because unit mistakes are the #1 avoidable error in astronomy problems.

Conversion factors = “multiply by 1”

A conversion factor is an equality written as a fraction.

Example:

\[1\,\text{m} \leftrightarrow 100\,\text{cm}\]

so you can use

\[\frac{100\,\text{cm}}{1\,\text{m}}=1 \quad \text{or} \quad \frac{1\,\text{m}}{100\,\text{cm}}=1.\]

1 min. Emphasize: conversion factor = 1. You’re not changing the quantity, just the label. This is the key insight for the factor-label method.

The factor-label method (foolproof)

1. Write what you’re given.

2. Multiply by conversion factors arranged so units cancel.

3. Check that your final units match what you wanted.

Selection rule

Put the unit you want to remove in the denominator.

Example: minutes → hours (structure, not memorization)

\[1000\,\text{min}\times\frac{1\,\text{hr}}{60\,\text{min}} = \frac{1000}{60}\,\text{hr}\approx 16.7\,\text{hr}\]

Sanity check: hours are bigger units than minutes, so the number should get smaller. ✓

Stop & Solve 2: Unit conversion chains

A) Convert \(60\,\text{mph}\) to \(\text{m/s}\).

B) Convert \(0.5^\circ\) to arcseconds.

(Use: \(1\,\text{mile}=1.6\,\text{km}\), \(1\,\text{hr}=3600\,\text{s}\), \(1^\circ=60\,\text{arcmin}\), \(1\,\text{arcmin}=60\,\text{arcsec}\).)

Quick vocab: angular units

Astronomers measure tiny angles in arcminutes (1/60 of a degree) and arcseconds (1/60 of an arcminute). The Moon is about 30 arcmin wide; a star’s disk is less than 0.05 arcsec.

→ Solution

Exponents matter in unit conversions

When a unit is squared or cubed, the conversion factor gets squared/cubed too.

The trap: Students often write

\[1\,\text{m}^3 = 100\,\text{cm}^3\] ❌

Why it’s wrong: You’re converting each dimension.

The right way:

\[1\,\text{m} = 100\,\text{cm}\]

\[1\,\text{m}^3 = (1\,\text{m})^3 = (100\,\text{cm})^3\]

\[= 100^3\,\text{cm}^3 = 10^6\,\text{cm}^3\] ✓

Rule: When converting \(\text{m}^n\), raise the conversion factor to the \(n\)th power too.

Pro tip: Parentheses are your best friend — wrap the number and unit together: \((100\,\text{cm})^3\), not \(100\,\text{cm}^3\).

2 min. This is a classic student trap. Show the trap first, ask “what’s wrong here?” Give them 10 seconds. Then reveal the right way. Walk through slowly. Emphasize: a cubic meter is a cube with sides of 100 cm each, so the volume is \(100 \times 100 \times 100\).

Compound Units: Building Blocks

Physics has only three base dimensions: length \([L]\), mass \([M]\), time \([T]\).

Everything else is built from combinations:

• Velocity = distance / time → \([L]/[T]\)
• Acceleration = velocity / time → \([L]/[T^2]\)
• Force = mass × acceleration → \([M][L]/[T^2]\)

The building principle

Complex quantities are just base dimensions multiplied and divided. If you know the recipe, you can always check your work.

1 min. Walk through how velocity becomes acceleration becomes force. This is dimensional analysis in miniature — combinations of base units.

Reference: Common Physical Quantities

Quantity	Dimension	SI Unit	Named Unit
Length	\([L]\)	m	meter
Mass	\([M]\)	kg	kilogram
Time	\([T]\)	s	second
Velocity	\([L][T]^{-1}\)	m/s	—
Acceleration	\([L][T]^{-2}\)	m/s²	—
Force	\([M][L][T]^{-2}\)	kg·m/s²	Newton (N)
Energy	\([M][L]^2[T]^{-2}\)	kg·m²/s²	Joule (J)
Power	\([M][L]^2[T]^{-3}\)	kg·m²/s³	Watt (W)
Pressure	\([M][L]^{-1}[T]^{-2}\)	kg/(m·s²)	Pascal (Pa)

Named units are shortcuts. A Newton is just kg·m/s². A Joule is just kg·m²/s². If a unit looks unfamiliar, rewrite it in base units!

30 sec. Don’t memorize this table — use it as a reference. The point: all units reduce to combinations of length, mass, and time.

Tool 3: The Ratio Method

Compare systems without calculator misery

0.5 min. Section transition. Let the tagline land.

Absolute vs. ratio (why ratios are magic)

The hard way: Calculate Jupiter’s surface gravity.

• Need: \(G = 6.67 \times 10^{-11}\,\text{N}\cdot\text{m}^2/\text{kg}^2\), mass, radius…
• Lots of numbers, easy to make mistakes.

The ratio way: Compare Jupiter to Earth.

• Jupiter is 318× Earth’s mass, 11× Earth’s radius
• We know Earth’s gravity (9.8 m/s²)

The pattern

If \(A = k B^n\), then comparing two cases:

\[\frac{A_2}{A_1}=\left(\frac{B_2}{B_1}\right)^n\]

The constant \(k\) cancels!

What this says: Ratios let you compare systems using only the relationship between quantities — no need to look up constants.

Scaling patterns you’ll use all semester

Scaling	Meaning	Where it shows up
\(\propto R^2\)	area grows fast	telescope area, surface area
\(\propto R^3\)	volume grows very fast	planet volumes, “how many Earths”
\(\propto 1/r^2\)	inverse-square	brightness, gravity

Worked Example: Telescope Collecting Area

Problem: The Keck telescope has a 10-meter diameter mirror. The Hubble Space Telescope has a 2.4-meter diameter mirror. How much more light can Keck collect?

Setup: Light-collecting area scales as \(A \propto D^2\) (area of a circle)

Ratio method: \[\frac{A_\text{Keck}}{A_\text{Hubble}} = \left(\frac{D_\text{Keck}}{D_\text{Hubble}}\right)^2 = \left(\frac{10}{2.4}\right)^2 \approx (4.2)^2 \approx 17\]

Answer: Keck collects about 17× more light than Hubble — no need to calculate actual areas!

2 min. Walk through step by step. Emphasize: we never needed to know \(\pi\) or calculate actual square meters. The ratio \(D_2/D_1\) does all the work. Students often want to compute \(\pi r^2\) for both — show them this shortcut.

Quick Check: Volume Ratio

The Sun’s radius is about 109× Earth’s radius. How many Earths fit inside the Sun?

Using \(V \propto R^3\), what is \(V_\odot / V_\oplus\)?

• About 109
• About 12,000
• About 1.3 million
• About 109 million

1-2 min. \(109^3 \approx 1.3 \times 10^6\). Key insight: volume grows as the cube of radius — much faster than area or length.

Answer: About 1.3 million

Applying the Pattern: Comparing Stars

What we measure: Brightness ratio of two stars (same apparent brightness)

What physics says: Inverse-square law means equal brightness at different distances implies different luminosities

What we conclude: A star 10× further away but equally bright must be 100× more luminous

The ratio shortcut

\(\frac{L_2}{L_1} = \left(\frac{d_2}{d_1}\right)^2 = 10^2 = 100\)

1 min. Second use of Observable → Model → Inference. Ratios + inverse-square = powerful tool for stellar comparison.

Inverse-square intuition (brightness)

If you move twice as far from a light source:

\[\text{brightness}\propto \frac{1}{d^2}\]

Watch the flip!

Because brightness is inversely proportional to \(d^2\), the ratio flips:

\[\frac{B_2}{B_1}=\left(\frac{d_1}{d_2}\right)^2\]

Credit: (A. Rosen/Gemini)

Astronomers call this flux — energy per second per area (W/m²).

Example: Twice as far → \(\dfrac{B_2}{B_1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\) the brightness.

2 min. Draw attention to the diagram. Light spreads over area = 4πd². Double the distance → 4× the area → 1/4 the brightness per unit area.

Worked Example: Mars Sunlight

Problem: Mars orbits at 1.5 AU from the Sun. Earth orbits at 1 AU. How does the intensity of sunlight on Mars compare to Earth?

Setup: Sunlight intensity follows the inverse-square law: \(I \propto 1/d^2\)

Ratio method: \[\frac{I_\text{Mars}}{I_\text{Earth}} = \left(\frac{d_\text{Earth}}{d_\text{Mars}}\right)^2 = \left(\frac{1}{1.5}\right)^2 = \left(\frac{2}{3}\right)^2 = \frac{4}{9} \approx 0.44\]

Answer: Mars receives only 44% as much sunlight as Earth — less than half!

This is why solar panels on Mars rovers need to be so large. (Mars is cold mostly because its thin atmosphere can’t trap heat — but less sunlight doesn’t help!)

2 min. Walk through carefully. Note the d terms flip because brightness is inversely proportional to d². Students often get confused about which distance goes on top — remind them: farther away = less light. Note: Mars is cold (−60°C average) mainly due to its thin atmosphere (~1% of Earth’s), not just distance. But less sunlight does mean solar panels must be larger.

Applying the Pattern: Distance from Brightness

What we measure: Brightness (flux \(F\)) — how much light arrives at our detector (W/m²)

What physics says: Inverse-square law relates flux, luminosity, and distance:

\[F = \frac{L}{4\pi d^2}\]

where \(L\) = luminosity (total power output, in Watts) and \(d\) = distance

What we conclude: If we know a star’s true luminosity \(L\) and measure its flux \(F\), we can solve for distance \(d\)

The inference chain

Observable (\(F\)) → Model (inverse-square) → Physical property (\(d\))

1 min. This is the first explicit use of the Observable → Model → Inference pattern. Refer back to Lecture 1. We’ll use this pattern all semester.

Tool 4: Rate Problems

Change per time is basically the universe’s favorite sentence structure

0.5 min. Section transition. Let the tagline land.

The rate template

Most rate problems are one equation with three rearrangements:

\[\text{amount} = \text{rate}\times\text{time}\]

• Find rate: \(\text{rate}=\dfrac{\text{amount}}{\text{time}}\)
  • “How fast?”
• Find time: \(\text{time}=\dfrac{\text{amount}}{\text{rate}}\)
  • “How long?”
• Find amount: \(\text{amount}=\text{rate}\times\text{time}\)
  • “How much/far?”

Astronomy examples

• Distance = speed × time
• Energy = power × time
• Mass loss = rate × time

What this says: If you know any two of these, you can find the third. This single pattern solves most “how far/fast/long” questions.

Worked Example: Building a Light-Year

Problem: How far does light travel in one year? (In meters)

Step 1: Identify the rate equation

\[\text{distance} = \text{speed} \times \text{time}\]

Step 2: Gather your values

• Speed of light: \(c = 3 \times 10^8\,\text{m/s}\)
• Time: \(1\,\text{year}\)

But wait — the units don’t match! We need time in seconds.

Step 3: Convert 1 year → seconds

\[1\,\text{yr} \times \frac{365\,\text{days}}{1\,\text{yr}} \times \frac{24\,\text{hr}}{1\,\text{day}} \times \frac{3600\,\text{s}}{1\,\text{hr}}\]

\[= 365 \times 24 \times 3600\,\text{s}\]

\[\approx 3.15 \times 10^7\,\text{s}\]

Worked Example: Building a Light-Year (continued)

Step 4: Multiply using scientific notation

\[1\,\text{ly} = c \times t = (3 \times 10^8\,\text{m/s}) \times (3.15 \times 10^7\,\text{s})\]

Scientific notation multiplication rule

Multiply coefficients, add exponents: \((a \times 10^m) \times (b \times 10^n) = (a \times b) \times 10^{m+n}\)

\[= (3 \times 3.15) \times 10^{8+7}\,\text{m}\] \[= 9.45 \times 10^{15}\,\text{m}\]

Answer: \(1\,\text{ly} \approx 9.5 \times 10^{15}\,\text{m}\) (about 9.5 trillion kilometers)

3 min total for both slides. Walk through each step deliberately. Emphasize: (1) unit conversion chain, (2) scientific notation multiplication rule, (3) units cancel (s/s = 1). This is a template for ALL rate problems: distance = speed × time.

Applying the Pattern: Lookback Time

What we measure: Distance to a galaxy (in light-years)

What physics says: Light travels at \(c = 3 \times 10^8\) m/s (finite speed)

What we conclude: A galaxy 2.5 million light-years away → we see it as it was 2.5 million years ago

Distance is a time machine. The further we look, the further back in time we see.

1 min. Third use of Observable → Model → Inference. Connect to the “distance = time dial” concept from Lecture 1.

Distance Is a Time Dial

Credit: (A. Rosen/NotebookLM)

1 min. Let the visual reinforce the concept. Each distance corresponds to a lookback time. Moon = 1.3 seconds ago; Sun = 8 minutes ago; Andromeda = 2.5 million years ago.

Stop & Solve 4: Earth’s orbital “speed”

Earth moves around the Sun at about \(29.8\,\text{km/s}\).

How far does Earth travel in one minute? (Answer in meters.)

→ Solution

Putting it together: a problem-solving checklist

The decoding ritual

For any quantitative astronomy question:

1. What am I finding? (write target with units)
2. What am I given? (write givens with units)
3. Pick the tool: conversion, ratio, or rate
4. Do the unit cancellation (this is your error detector)
5. Sanity check: bigger unit → smaller number? right power of ten?

The Cosmic Distance Ladder

Credit: (A. Rosen/NotebookLM)

1 min. Preview of coming attractions. Each rung calibrates the next. We’ll explore this in detail in Module 2. For now, just note the pattern.

Quick Reference: Astronomy unit ladder

Unit	What it’s good for	Useful fact
AU	solar system distances	\(1\,\text{AU}\approx 1.50\times10^{11}\,\text{m}\)
ly	“how far light goes”	\(1\,\text{ly}\approx 9.46\times10^{15}\,\text{m}\)
pc	star/galaxy distances	\(1\,\text{pc}\approx 3.09\times10^{16}\,\text{m}\approx 3.26\,\text{ly}\)

What to Take Away

Recognition, not retention

You don’t need to memorize formulas. You need to recognize patterns:

• Powers of ten compress cosmic scales
• Ratios reveal relationships without constants
• Units keep your equations honest
• Rates connect distance, time, and speed

When you see a big number or a scaling question, you’ll know which tool to reach for.

1 min. Reinforce: this is a toolkit, not a test. Recognition matters more than memorization.

Exit Ticket

If you move twice as far from a light source, brightness becomes…

• Half (1/2)
• One-quarter (1/4)
• One-eighth (1/8)
• The same

30 seconds. Quick pulse check before dismissal. Inverse-square: \(1/2^2 = 1/4\).

Solutions

Use these only if you want to show a full worked path. Otherwise keep momentum.

Solution 0

• \(2\,\text{AU}\): \(2\times 8.3\,\text{min}\approx 16.6\,\text{min}\)
• \(0.5\,\text{AU}\): \(0.5\times 8.3\,\text{min}\approx 4.15\,\text{min}\)

← Back

30 sec. Simple proportional reasoning — distance scales linearly with light-time.

Solution 1

Step 1: Multiply the coefficients \[3 \times 4 = 12\]

Step 2: Add the exponents \[10^5 \times 10^3 = 10^{5+3} = 10^8\]

Step 3: Combine \[12 \times 10^8\]

Step 4: Normalize (coefficient should be between 1 and 10) \[12 \times 10^8 = 1.2 \times 10^9\]

← Back

1 min. Walk through each step deliberately. The normalization step catches students — remind them that \(12 = 1.2 \times 10^1\), so we add 1 to the exponent.

Solution 2

A) \(60\,\text{mph} \to \text{m/s}\)

\[60 \frac{\text{mile}}{\text{hr}}\times\frac{1.6\,\text{km}}{1\,\text{mile}}\times\frac{1000\,\text{m}}{1\,\text{km}}\times\frac{1\,\text{hr}}{3600\,\text{s}}\approx 26.7\,\text{m/s}\]

B) \(0.5^\circ \to \text{arcsec}\)

\[0.5^\circ\times\frac{60\,\text{arcmin}}{1^\circ}\times\frac{60\,\text{arcsec}}{1\,\text{arcmin}}=1800\,\text{arcsec}\]

← Back

45 sec. Emphasize unit cancellation — watch the units disappear step by step.

Solution 3

\[109^3 \approx (1.09\times10^2)^3 = 1.09^3\times10^6\approx 1.3\times10^6.\]

So the Sun’s volume is about 1.3 million Earth volumes.

← Back

30 sec. The cube makes a huge difference — radius ratio of 109 becomes volume ratio of 1.3 million.

Solution 4

\[29.8\,\text{km/s} = 2.98\times10^4\,\text{m/s}\]

One minute is \(60\,\text{s}\), so

\[\text{distance}=vt=(2.98\times10^4\,\text{m/s})(60\,\text{s})\approx 1.79\times10^6\,\text{m}.\]

That’s about 1800 km in one minute.

← Back

30 sec. Rate × time = distance. Earth covers almost 2000 km every minute — cosmic speeds are fast!