The Sky Is a Map

Celestial Geometry, Seasons,
and Angular Size

Dr. Anna Rosen

January 26, 2026

Join iClicker

Credit: iClicker

join.iclicker.com/ASES

If you can’t scan: open the link and enter the course code ASES.

30–60 sec. Get everyone connected before starting.

Credit: (A. Rosen/Gemini)

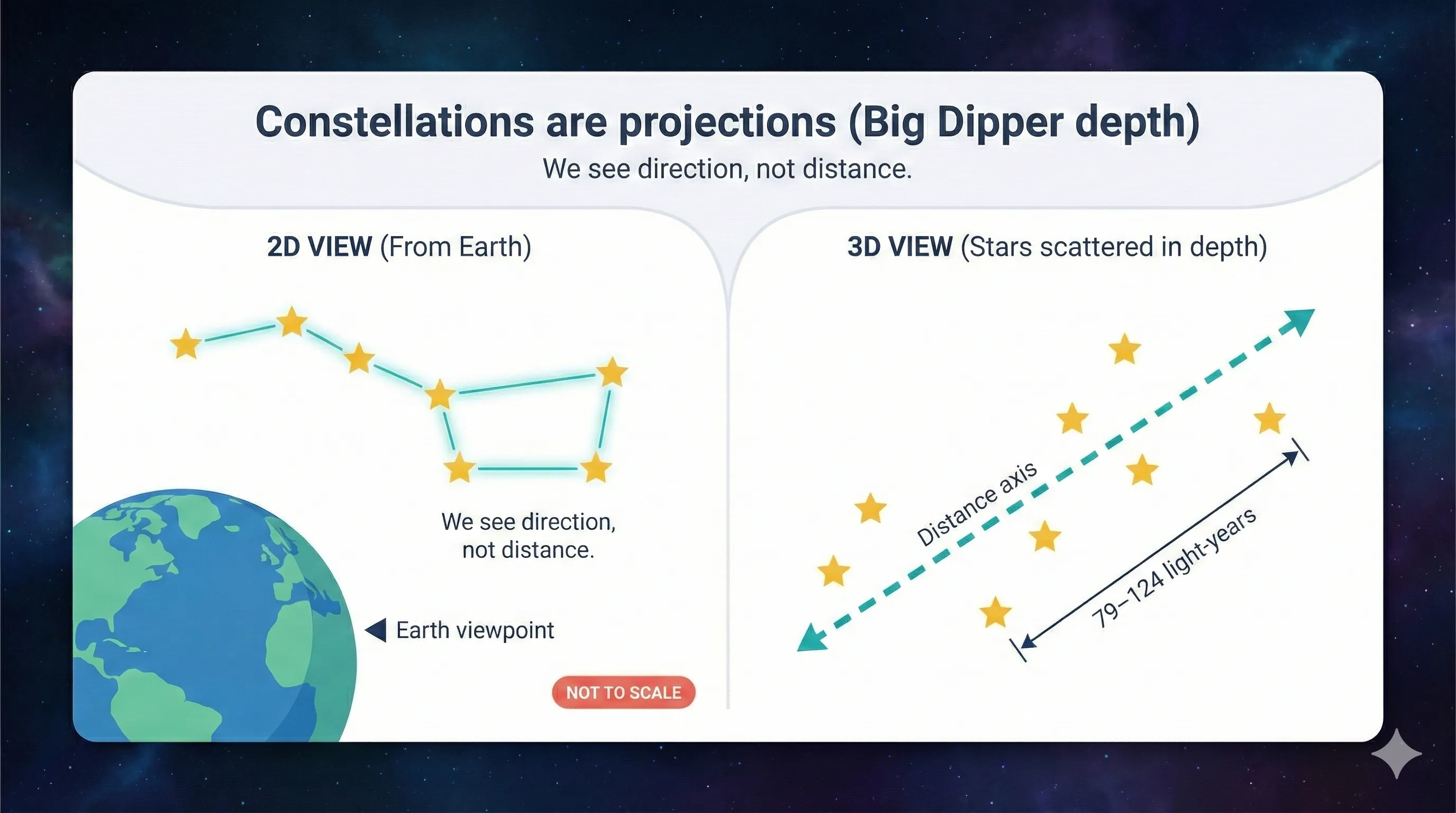
The Big Dipper looks like a family.

But these stars aren’t neighbors in space.

They range from 79 to 124 light-years away.

The pattern exists only because they lie along similar directions from Earth.

0–2 min. Let the image speak first.

“When you look at the Big Dipper, your brain sees a pattern — a group. But space is 3D, and you’re seeing a 2D projection. These stars just happen to be in the same general direction.”

Today’s Learning Objectives

By the end of today, you’ll be able to:

• Explain why the sky is a map of directions, not distances
• Use the celestial sphere to locate objects: horizon, zenith, poles, equator, ecliptic
• Explain seasons as axial tilt (sun angle + day length), not changing distance
• Interpret solstices and equinoxes geometrically
• Use angular size reasoning to compare sizes and distances

2–3 min. Frame the day: “Today is about geometry. If you can draw it, you can understand it.”

The Celestial Sphere

A Map of Directions

3 min. Section transition. Brief pause.

The Problem: No Depth Perception

Look up at the night sky. You see points of light scattered across a dark dome.

Here’s the fundamental problem:

Your eyes can’t tell you whether a star is
close and dim or far and luminous.

The sky gives us directions by default.
Measuring distances requires extra work.

3–4 min. “This isn’t a limitation — it’s a starting point. We embrace what the sky naturally gives us: a coordinate system for pointing at things.”

The Celestial Sphere

Credit: (A. Rosen/Gemini)

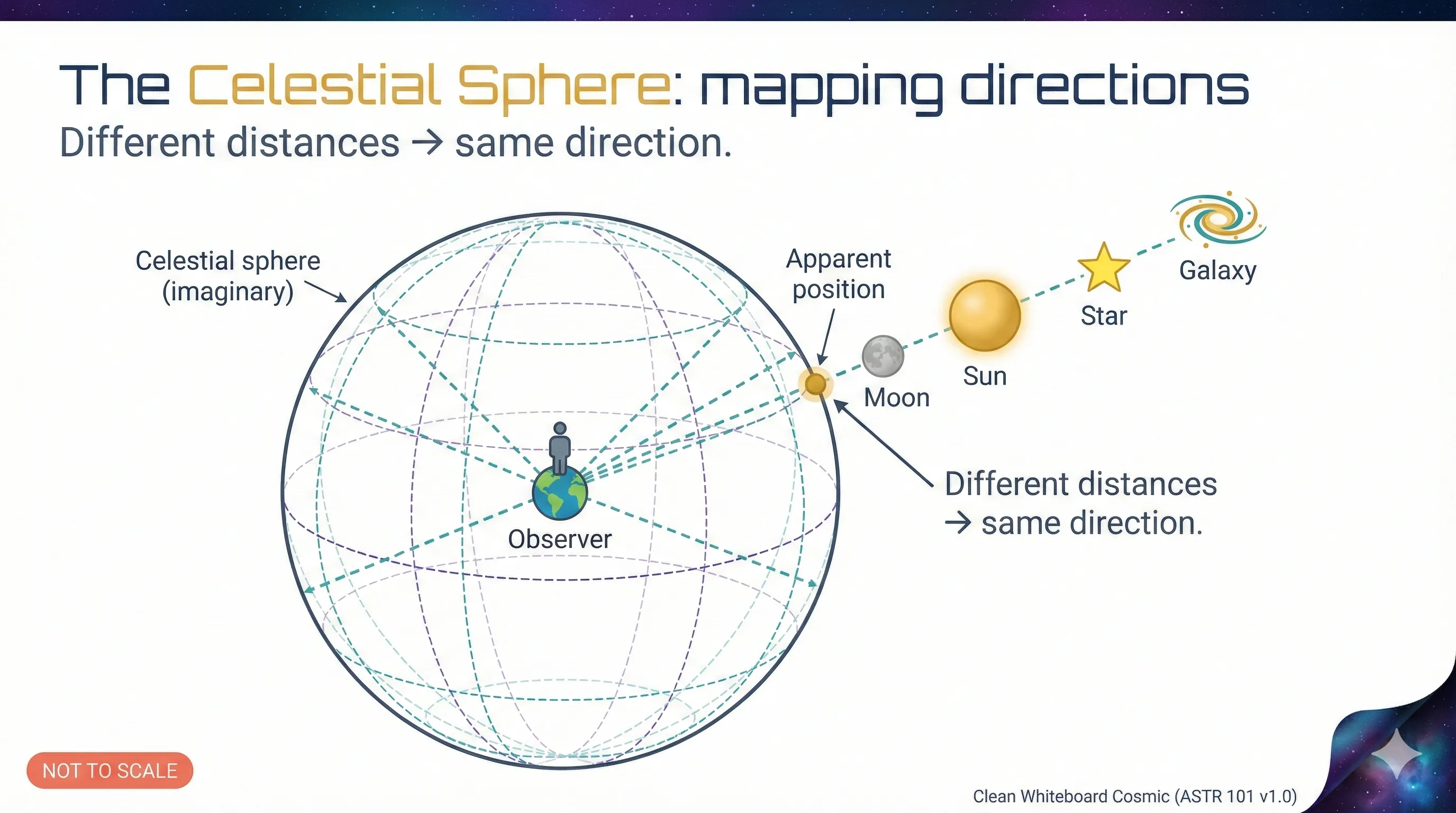
Imagine standing at the center of a vast, transparent globe.

Every star, planet, and galaxy can be located by pointing in some direction.

Key insight: The celestial sphere doesn’t represent where things are — it represents where to look.

4–5 min. “It’s a direction-finder, not a distance-finder. Objects at wildly different distances get mapped to the same sphere.”

Reference Points on the Sky

Credit: (A. Rosen/ChatGPT)

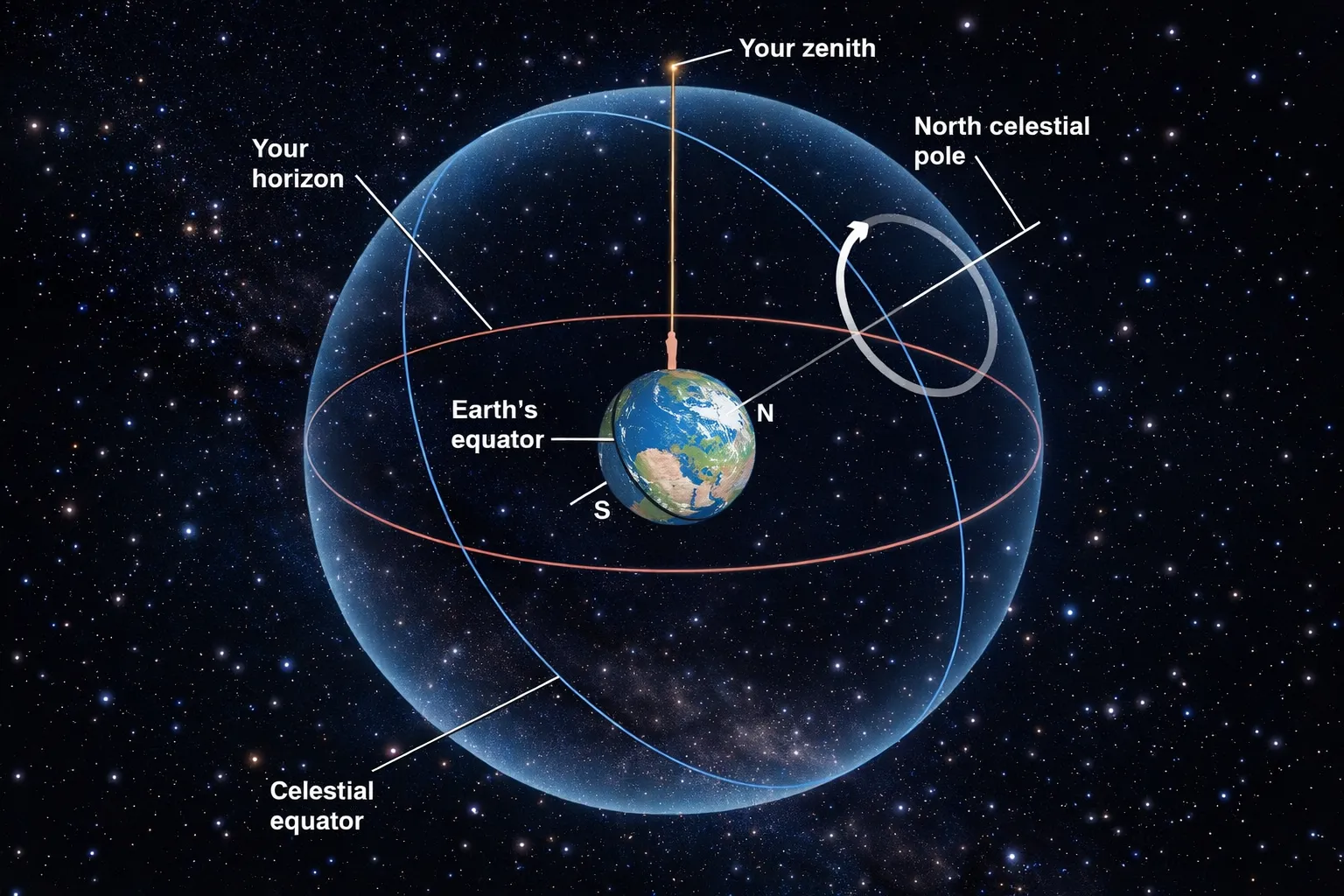
Point	What It Is
Zenith	Straight up from where you stand
Celestial poles	Earth’s rotation axis extended to the sky

Zenith is your local “up.”

North is a compass direction along the horizon — not the same as zenith!

5–6 min. Common confusion: students mix up “zenith” and “north.” Emphasize: zenith is straight up, north is along the horizon.

Reference Circles on the Sky

Circle	Definition	What It Corresponds To
Celestial equator	Earth’s equator projected onto the sky	Divides N/S celestial hemispheres
Horizon	Where sky meets ground	Your local view (depends on location)
Ecliptic	Sun’s yearly path across the sky	Earth’s orbital plane projected onto sky

All three are great circles — they divide the celestial sphere into equal halves.

6–7 min. “These aren’t arbitrary — they’re defined by Earth’s rotation (equator) and orbit (ecliptic).”

Celestial Coordinates

Coordinate	Meaning	Earth Analog
Declination (Dec)	Angle N/S of celestial equator (−90° to +90°)	Latitude
Right Ascension (RA)	Position along equator (0–24h)	Longitude

Why hours for RA?

24 hours = 360°, so 1 hour = 15°.

The sky appears to rotate once per day — hours match the clock.

Observable: Position on the sky (RA, Dec)

Model: Celestial sphere geometry

Inference: Where to point the telescope tonight

7–8 min. Don’t dwell on RA details — just establish the analogy to lat/long.

Two Circles That Matter

Credit: (A. Rosen/ChatGPT)

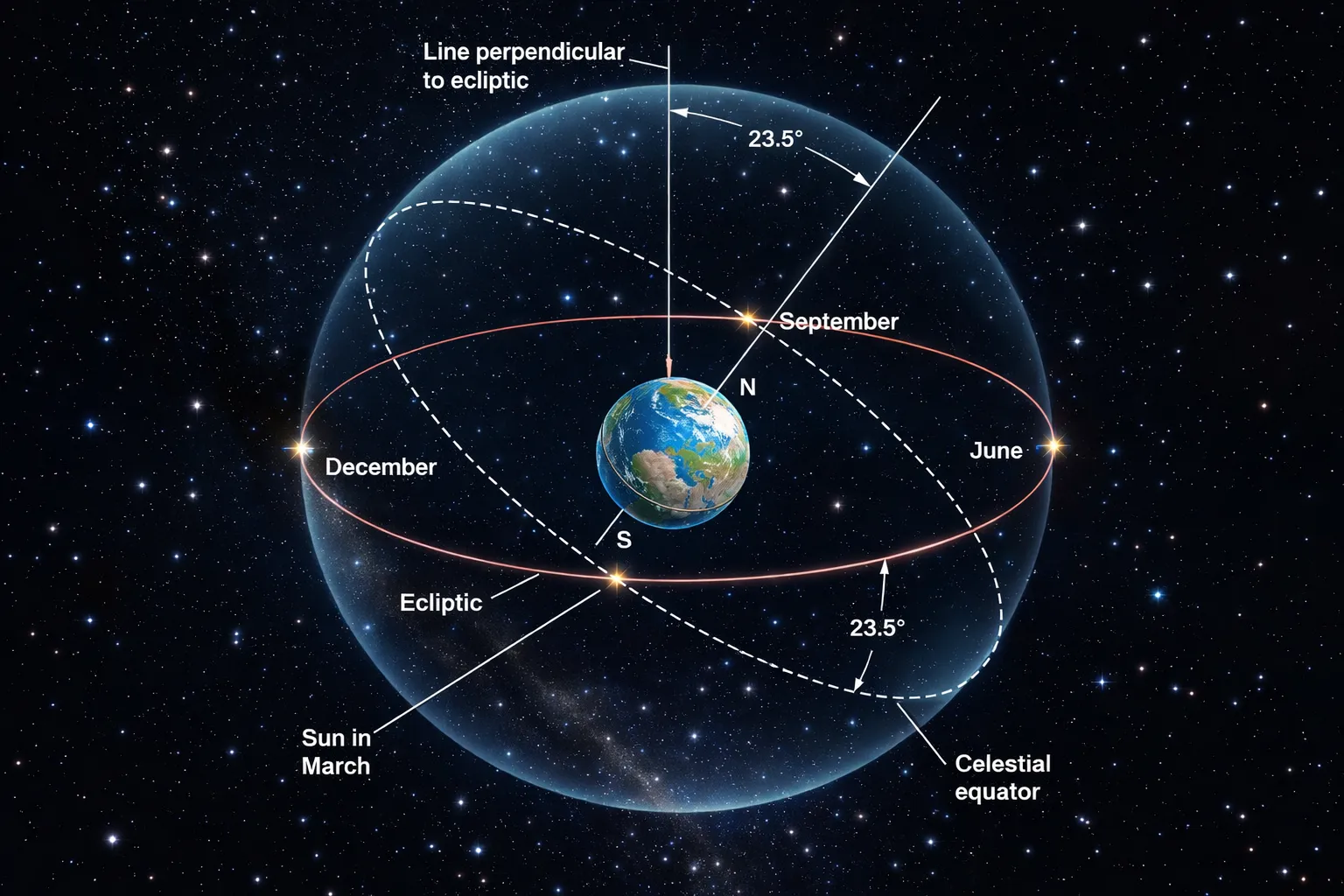
Celestial Equator: Defined by Earth’s rotation — perpendicular to the spin axis.

Ecliptic: Defined by Earth’s orbit — the Sun’s apparent yearly path.

The crucial point: These circles are tilted 23.5° relative to each other.

This tilt is why we have seasons.

8–9 min. “Two different motions — rotation and orbit — define two different reference planes. They don’t align, and that misalignment changes everything.”

Two Motions, Two Time Scales

Motion	Cause	Time Scale	What You See
Daily arc	Earth’s rotation	24 hours	Sun rises east, sets west
Yearly drift	Earth’s orbit	365 days	Sun slides eastward along ecliptic

The daily arc is why the Sun is up during the day.

The yearly drift is why the Sun’s noon altitude changes with the seasons.

9–10 min. “When we talk about the Sun’s position ‘changing with seasons,’ we mean along the ecliptic — the yearly drift, not the daily motion.”

Quick Check: The Ecliptic

The ecliptic is:

• The path the Moon takes across the sky each night
• The Sun’s apparent path across the sky over the course of a year
• The same as the celestial equator
• The edge of Earth’s shadow

10–11 min. Give 30 seconds.

Correct: B. The ecliptic traces Earth’s orbital plane — the Sun appears to move along it over a year.

Seasons: Tilt, Not Distance

The Misconception That Won’t Die

11 min. Section transition. “Now we apply the geometry.”

The Common Misconception

Credit: (A. Rosen/Gemini)

“Earth is closer to the Sun in summer.”

This is wrong — but it’s a reasonable first guess.

Surveys show many college students and adults believe this.

11–12 min. Don’t shame — acknowledge it’s intuitive. “It makes sense! Closer = warmer, right? But nature doesn’t cooperate.”

The Proof: Opposite Hemispheres

If distance caused seasons:

Both hemispheres would have summer at the same time — when Earth is closest to the Sun.

What we observe:

When it’s summer in the Northern Hemisphere, it’s winter in the Southern Hemisphere.

The hemispheres have opposite seasons.

Conclusion: Distance cannot be the cause.

12–13 min. “This is the killer observation. One fact rules out the entire hypothesis.”

The Numbers Don’t Work Either

• Earth’s distance from the Sun varies by only ~3% over the year
• Perihelion (closest): 147 million km — in January
• Aphelion (farthest): 152 million km — in July
• This 3% distance change affects solar flux by only ~7%

The irony: Earth is farthest from the Sun during Northern Hemisphere summer!

13–14 min. “The effect is too small AND in the wrong direction for the Northern Hemisphere.”

The Real Mechanism: Effect 1

Credit: (A. Rosen/NotebookLM)

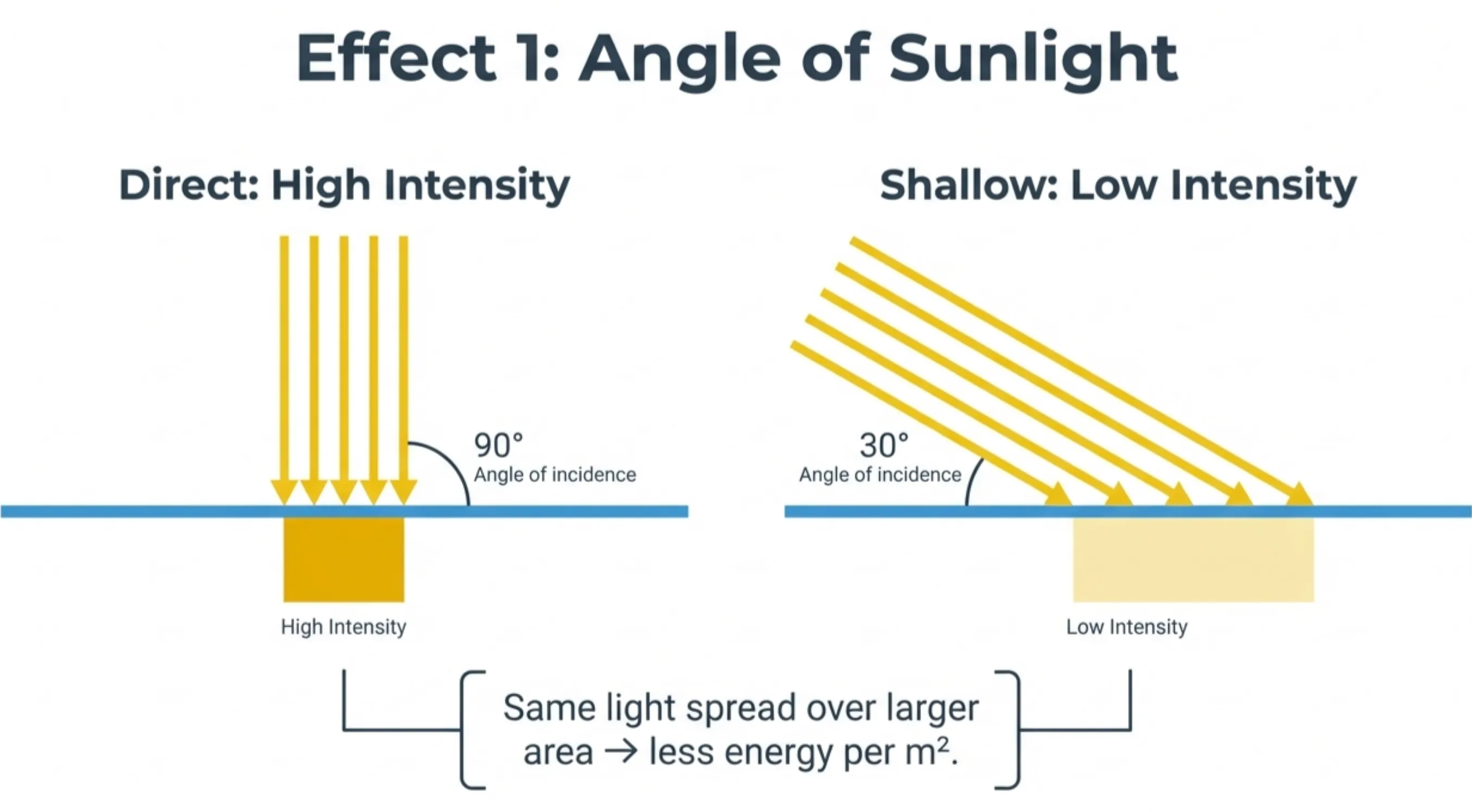
Sunlight Angle

When the Sun is higher in the sky, its rays hit the ground more directly.

Flashlight analogy:

• Straight down → bright circle
• Tilted → same light spreads over larger area
• Less energy per square meter

14–15 min. “Effect 1: sun angle. Higher sun = more concentrated energy.”

The Real Mechanism: Effect 2

Credit: (A. Rosen/NotebookLM)

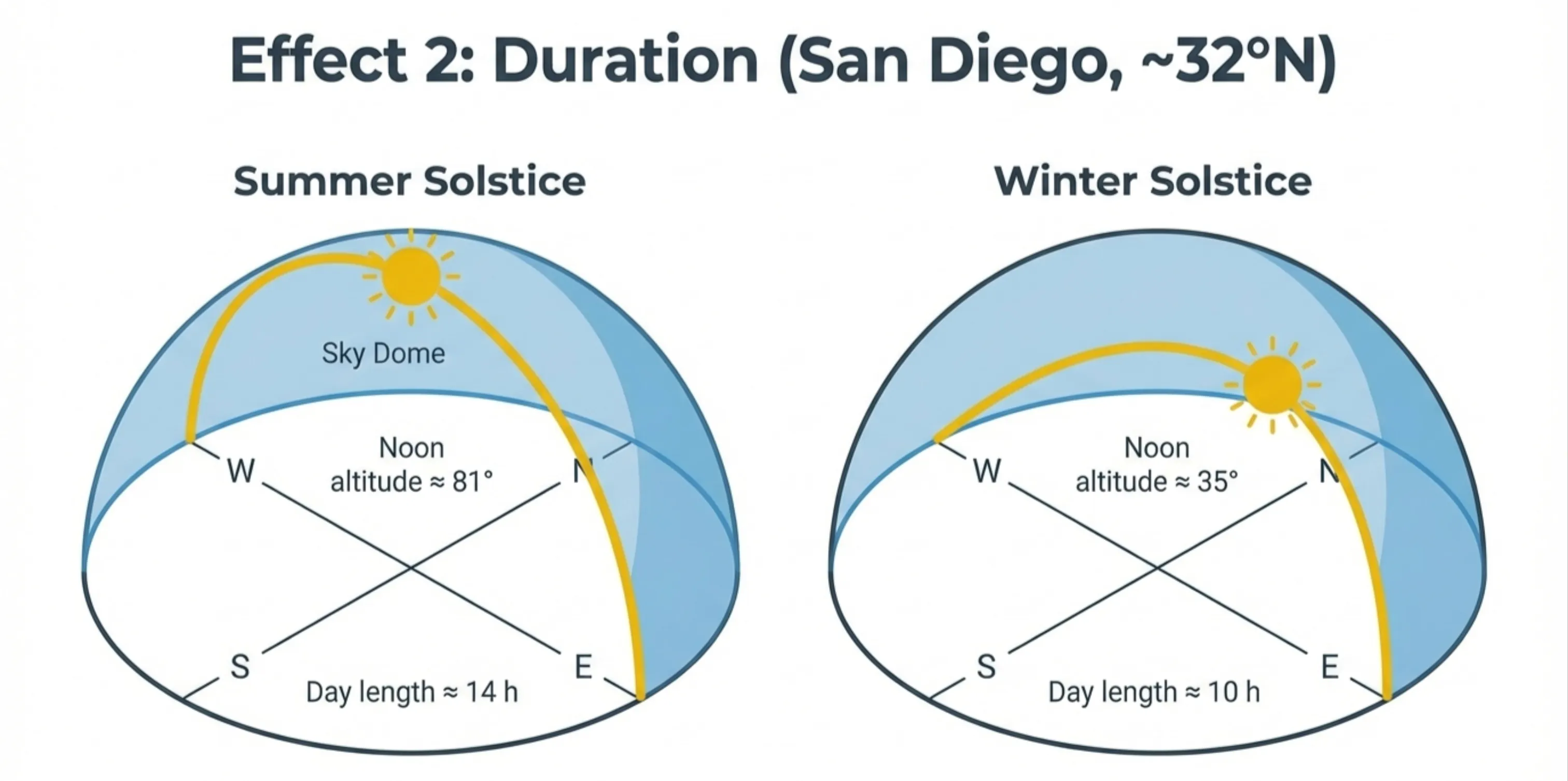
Day Length

When your hemisphere tilts toward the Sun, the Sun takes a longer path across your sky.

San Diego (~32°N):

Season	Day Length	Noon Altitude
Summer solstice	~14 hours	~81°
Winter solstice	~10 hours	~35°

15–16 min. “Effect 2: day length. More hours of heating. The combination is powerful — 4 extra hours of more direct sunlight.”

The Bottom Line

Credit: (A. Rosen/NotebookLM)

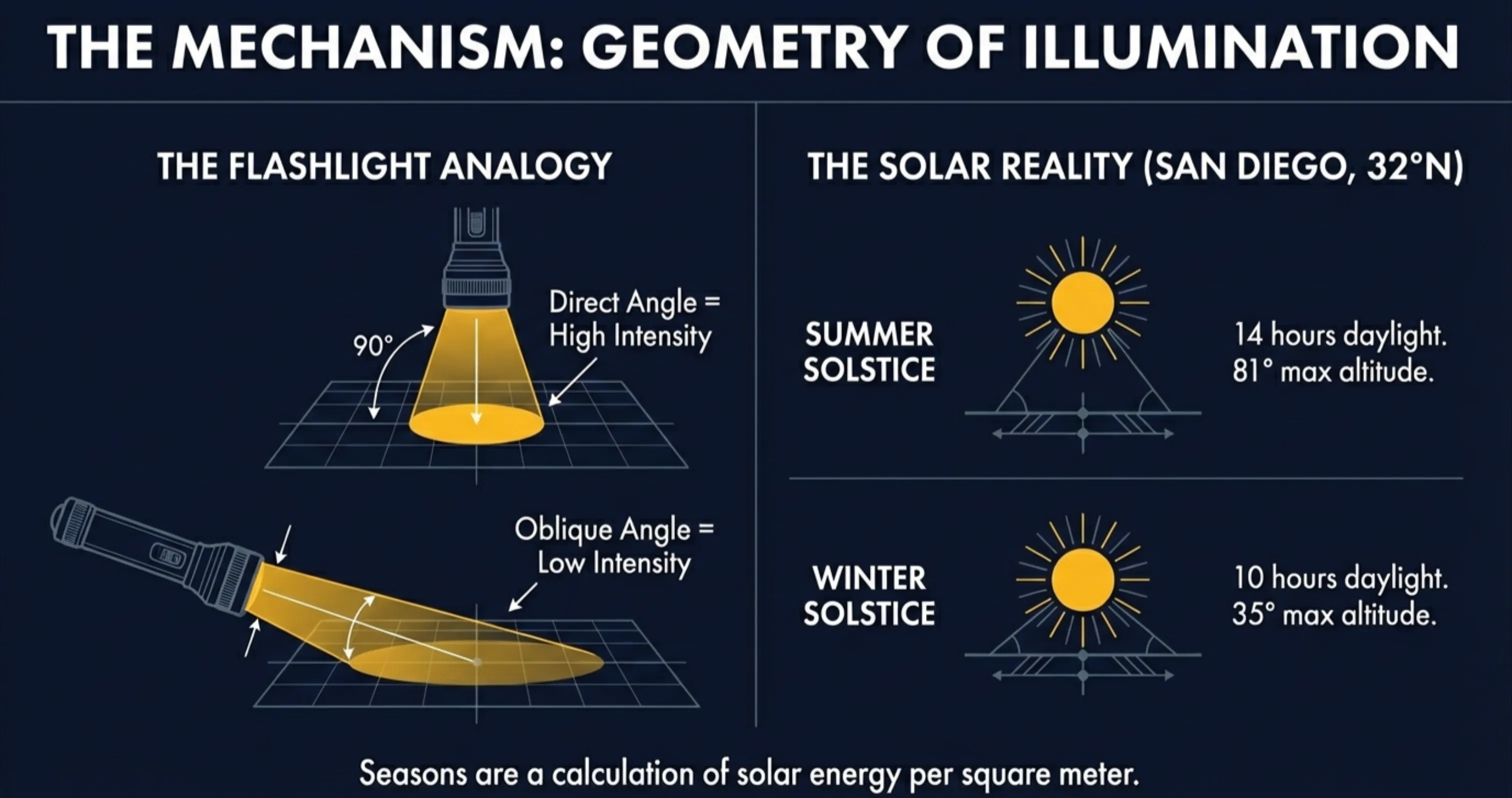
Observable: Sun’s noon altitude and day length change through the year

Model: Earth’s 23.5° axial tilt

Inference: Seasons are about solar energy per square meter per day

Tilt changes this through:

1. Sun angle (how concentrated)
2. Day length (how many hours)

16–17 min. “This is the complete answer. Tilt creates two geometric effects that combine to make seasons.”

Quick Check: Summer Sun Path

During summer in your hemisphere, the Sun:

• Is closer to Earth and appears larger
• Rises and sets at the same points as in winter, just brighter
• Takes a higher, longer path across the sky
• Moves faster across the sky

17–18 min. Give 30 seconds.

Correct: C. Higher path (more direct energy) + longer path (more hours of heating).

Solstices and Equinoxes

Credit: (A. Rosen/ChatGPT)

Equinox = day ≈ night everywhere

Solstice = Sun “stands still” at extreme

Event	Date	What Happens
March Equinox	~Mar 20	Sun crosses equator going north
June Solstice	~Jun 21	Sun farthest north; longest NH day
Sept Equinox	~Sep 22	Sun crosses equator going south
Dec Solstice	~Dec 21	Sun farthest south; shortest NH day

18–19 min. “Four special geometry days. The ecliptic and equator intersect at equinoxes; the Sun reaches its extremes at solstices.”

Demo: Seasons Explorer

Open: astrobytes-edu.github.io/astr101-sp26/demos/seasons/

Demo Mission 1: Test the Distance Hypothesis

• Click through the 4 season presets
• Record the Earth-Sun Distance for each
• Is Earth closer during NH summer or winter?

(You should find Earth is farthest from the Sun in July — the opposite of what distance hypothesis predicts!)

19–21 min. Have students follow along on their devices if possible. This is active learning.

Demo Mission 2: The Real Mechanism

With display overlays on:

• Go to June Solstice vs December Solstice
• Record Day Length and Sun Altitude for both

Season	Day Length	Sun Altitude
June Solstice	_____	_____
December Solstice	_____	_____

Key question: What changes between June and December that explains the temperature difference?

21–23 min. “Day length and sun altitude both change dramatically. Distance barely changes. Case closed.”

Angular Size

How Big Things Look

23 min. Section transition.

The Fundamental Insight

Credit: (A. Rosen/NotebookLM)

How big is the Moon?

In kilometers: 3,474 km diameter.

But that’s not what you see.

What you see is how much of your field of view it occupies — its angular size.

The Moon’s angular size: ~0.5°

23–24 min. “Angular size is the angle an object subtends. It depends on both physical size AND distance.”

Angular Units

Unit	Relation	Example
1 degree (°)	Base unit	Thumb width at arm’s length ≈ 2°
1 arcminute (’)	1° = 60’	Human eye resolution ≈ 1’
1 arcsecond (“)	1’ = 60”	Telescope territory

Useful conversion:

0.5° = 30’ = 1800”

Credit: (A. Rosen/NotebookLM)

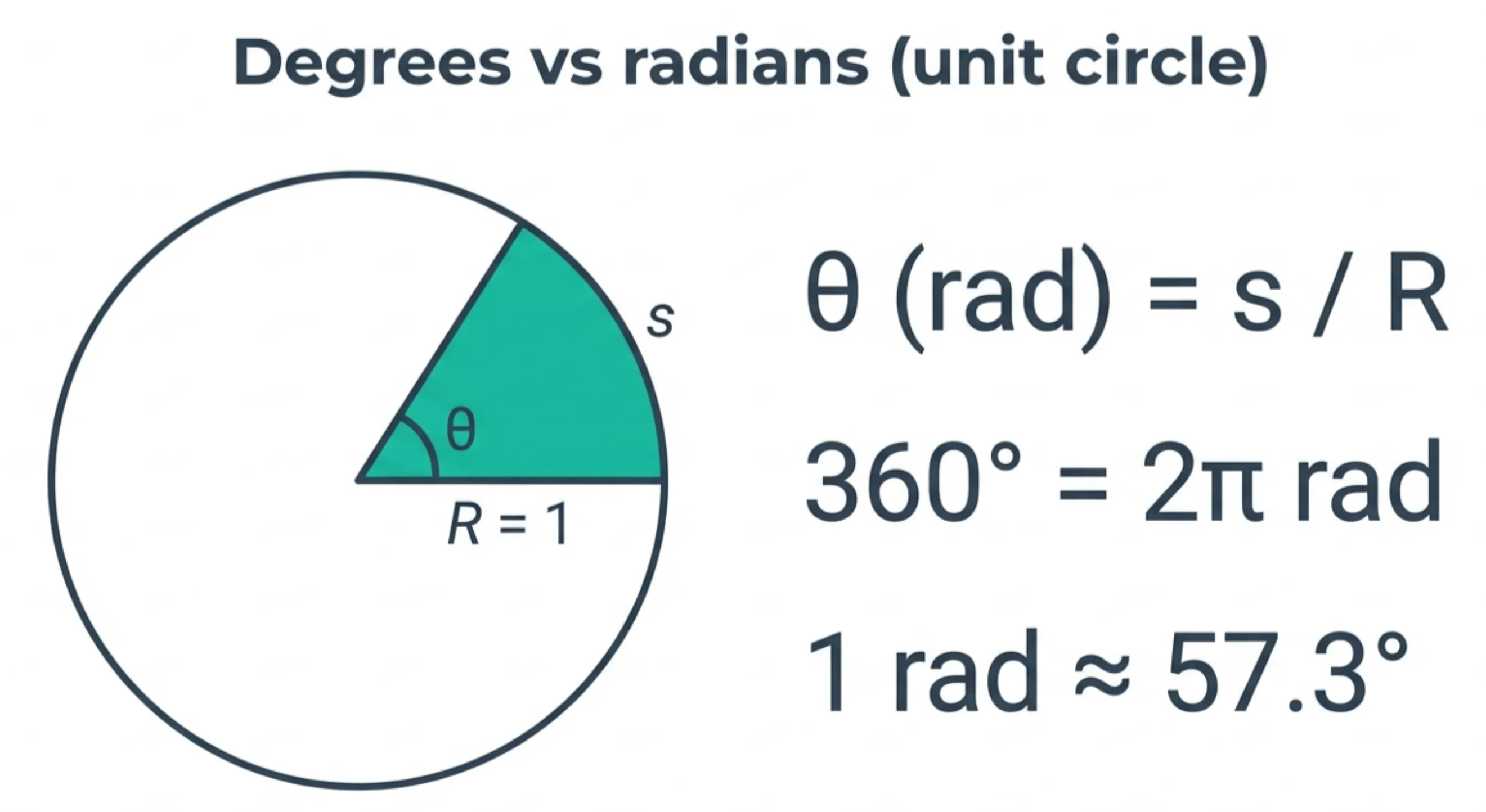
A radian is defined by \(θ =\) arc/radius.

1 radian ≈ 57.3°

24–25 min. “Degrees for big stuff, arcminutes and arcseconds for small stuff. Astronomers use arcseconds for tiny angles.”

The Small-Angle Formula

For small angles (less than a few degrees):

\[\boxed{\theta = \frac{D}{d} \quad \text{(radians)}}\]

To convert to degrees:

\[\boxed{\theta_{\text{degrees}} = 57.3° \times \frac{D}{d}}\]

where \(D\) = physical diameter, \(d\) = distance

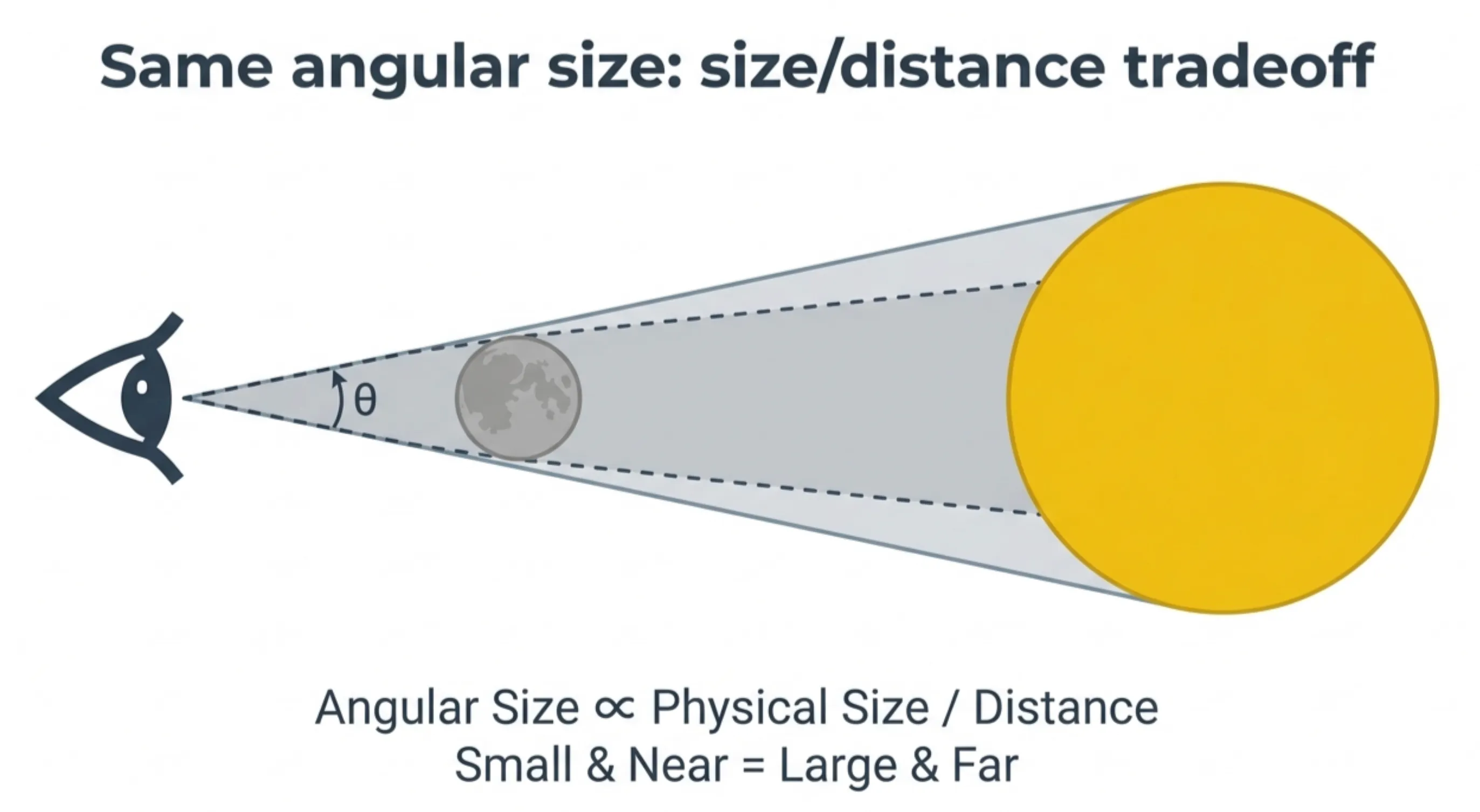
Key insight: Angular size depends on both physical size and distance.

A large object far away can look the same as a small object nearby.

25–26 min. “This formula is the heart of angular size reasoning. Size divided by distance.”

Worked Example: The Moon

• Moon’s diameter: \(D = 3474\) km
• Moon’s distance: \(d = 384{,}000\) km
• Angular size: \(\theta = 57.3° \times \frac{3474 \text{ km}}{384{,}000 \text{ km}} = 57.3° \times 0.00905\)
• Result: θ ≈ 0.52° (about half a degree)

That’s roughly half the width of your pinky finger at arm’s length.

26–27 min. Walk through the calculation. “The formula works — and it matches what we see.”

The Sun-Moon Coincidence

The Sun:

• Diameter: ~1,400,000 km
• Distance: ~150,000,000 km
• Angular size: ~0.53°

The Moon:

• Diameter: ~3,474 km
• Distance: ~384,000 km
• Angular size: ~0.52°

The Sun is 400× larger but also 400× farther.

The factors cancel — they appear almost exactly the same size!

27–28 min. “This is a cosmic coincidence. No law of physics requires this — it’s just where we happen to be in history.”

Why This Matters

Because of this coincidence, the Moon can just barely cover the Sun completely.

Total solar eclipses are possible.

We see the Sun’s corona — its outer atmosphere — only during these moments.

28–29 min. “If the Moon were smaller or farther, we’d never see totality. This coincidence is why eclipses are so spectacular.”

Quick Check: Same Angular Size

Two planets have the same angular size as seen from Earth. This means:

• They have the same physical diameter
• They are at the same distance
• The ratio of their diameters equals the ratio of their distances
• They have the same luminosity

29–30 min. Give 30 seconds.

Correct: C. Same angular size means the size-to-distance ratio is the same.

Demo: Angular Size Explorer

Open: astrobytes-edu.github.io/astr101-sp26/demos/angular-size/

Explore:

• Double the distance → what happens to angular size?
• Double the physical size → what happens to angular size?
• Compare Sun vs Moon (Today) presets
• Watch the unit label (° / ′ / ″) when angles are tiny

You should find: distance ×2 → angular size ÷2 (inverse relationship)

30–32 min. Quick hands-on demo. “Verify the formula with your own eyes.”

A Cosmic Privilege

• The Moon is drifting away from Earth at 3.8 cm per year
• We measure this with laser retroreflectors left by Apollo astronauts
• Billions of years ago, the Moon appeared much larger
• In ~600 million years, the Moon will appear too small to fully cover the Sun

We live in a privileged cosmic moment: the only era when total solar eclipses are possible.

32–33 min. “In the past, annular eclipses weren’t possible because the Moon was too big. In the future, total eclipses won’t be possible because the Moon will be too small. We’re lucky.”

Connecting the Concepts

33 min. Section transition to wrap-up.

The Through-Line: Geometry

• Celestial sphere: The geometry of directions in the sky
• Seasons: The geometry of illumination from Earth’s tilt
• Angular size: The geometry of apparent size from distance

Observable: Positions, angles, apparent sizes

Model: 3D geometry of Earth, Sun, Moon, stars

Inference: Real physical properties and motions

33–34 min. “All of today’s concepts are geometry. If you can draw it, you can understand it.”

Looking Ahead: Lecture 4

Next time: Moon Phases and Eclipses

We’ll apply angular size to understand:

• Why the Moon appears to change shape each month
• Why eclipses don’t happen every month
• The difference between total, annular, and partial eclipses

Preview: Moon phases are NOT caused by Earth’s shadow. (The geometry will prove it.)

34–35 min. “Everything you learned today — celestial sphere, angular size — comes back in Lecture 4.”

Takeaways

What to recognize:

1. The sky is a map of directions, not distances — that’s the celestial sphere
2. Seasons are caused by axial tilt (sun angle + day length), not distance
3. Angular size depends on both physical size AND distance
4. The Sun-Moon angular size match is a coincidence that enables total eclipses

Recognition, not retention — you should be able to identify these ideas when they return.

35–37 min. “You don’t need to memorize formulas. You need to recognize these patterns when you see them.”

Reading & Practice

Before next class:

• Complete the Lecture 3 Reading (includes demo explorations)
• Work through the Check Yourself questions (some will be assigned for homework)
• Try at least 3 Practice Problems
• Read or skim the Lecture 4 Reading

Questions?

37–38 min. Point them to resources.

38–40 min. Open floor for questions. If none, dismiss with: “See you next time for moon phases and eclipses!”