The Cosmic Messenger

Light Carries Information

Dr. Anna Rosen

February 9, 2026

You’ve never touched a star.

You never will.

Yet you know its temperature, composition, age, mass, and motion.

How?

0–1 min. Let the question hang. “The answer is light.”

Light is the universe’s messenger

Light is the universe’s messenger.

Every photon has a story:

• Its wavelength reveals temperature
• Spectral shifts reveal motion
• Specific wavelengths reveal composition

1–2 min. “Light is how the universe communicates with us.”

From Observables to Inference

Credit: (A. Rosen/NotebookLM)

For any star, we measure:

• brightness
• position
• wavelength
• timing

Then infer temperature, composition, motion, and planetary context.

Use this as a concrete anchor for “astronomy by inference.”

Today’s Learning Objectives

By the end of today, you can:

• Describe light as an electromagnetic wave (\(c = \lambda \nu\))
• Identify the major regions of the electromagnetic spectrum
• Explain why the sky is blue and sunsets are red

Today’s Learning Objectives (continued)

By the end of today, you can:

• Explain why lunar eclipses produce a red Moon
• Apply the inverse-square law for light intensity (\(I \propto 1/r^2\))
• Infer temperature, composition, and motion from starlight observations

2–3 min. “Today is about what light IS and why wavelength matters.”

Where We Left Off

Lectures 5-6: Motion reveals mass

• Kepler found patterns in planetary motion
• Newton explained those patterns with gravity
• By measuring orbits, we can “weigh” invisible objects

Today: Light reveals everything else — temperature, composition, velocity, distance.

3–4 min. “Motion reveals mass. Light reveals everything else.”

Part 1: What Is Light?

The electromagnetic wave

Light Is an Electromagnetic Wave

Credit: Illustration: NASA, ESA, CSA

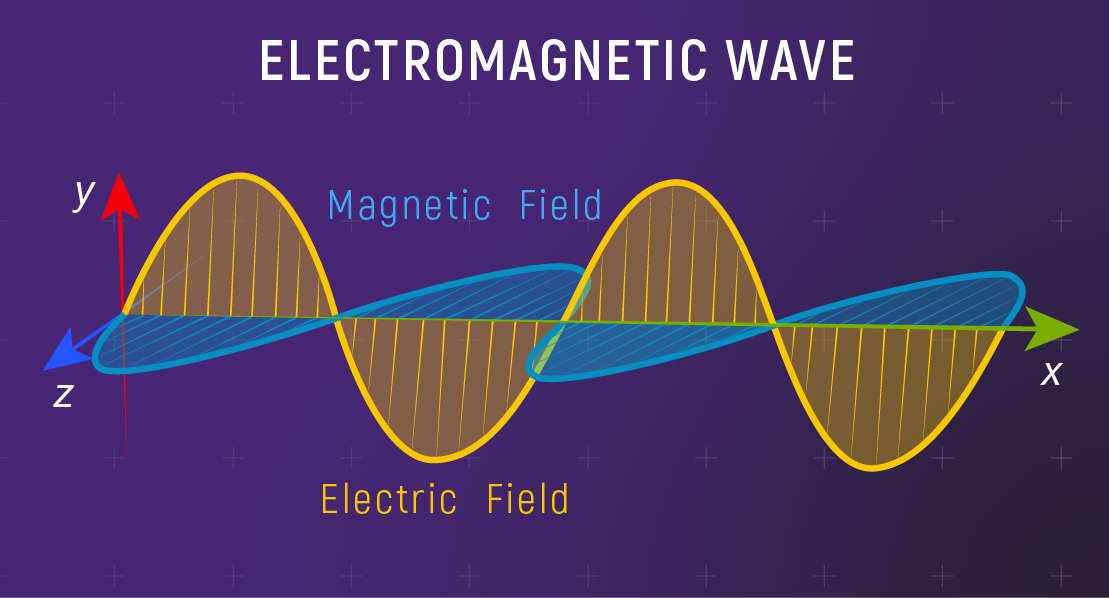
Electromagnetic wave:

Self-propagating oscillation of electric and magnetic fields.

Unlike sound or ocean waves — no medium needed!

Light travels perfectly through the vacuum of space.

4–5 min. “This is why we can see starlight from billions of light-years away.”

Mechanical vs Electromagnetic Waves

Credit: Illustration: NASA, ESA, CSA

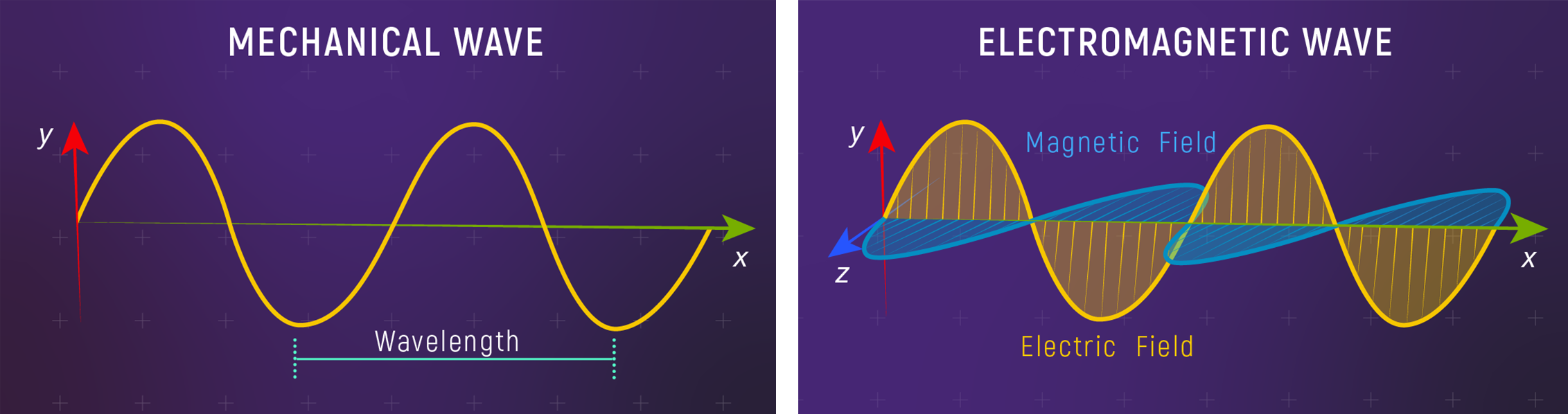
EM waves need no material medium, so light crosses interstellar vacuum.

Keep this slide visual-first; one sentence is enough.

Two Key Properties

Property	Symbol	What it measures	Units
Wavelength	\(\lambda\)	Distance between wave crests	meters (m) or nanometers (nm)
Frequency	\(\nu\)	Wave crests passing per second	hertz (Hz)

Wave relation: \(c = \lambda \nu\) (with \(c = 3 \times 10^8\ \mathrm{m/s}\))

5–6 min. “Wavelength and frequency are the two key descriptors.”

Predict First!

Without doing math: if the wavelength doubles (\(\lambda \to 2\lambda\)), the frequency \(\nu\) becomes…

1. \(2\times\)

2. \(\frac{1}{2}\times\)

3. unchanged

4. \(4\times\)

30 s. Commit first. Then reveal with \(c=\lambda \nu\): since \(c\) is constant, doubling \(\lambda\) halves \(\nu\).

The Wave Equation

\[c = \lambda \nu\]

Since \(c\) is constant:

• Longer wavelength means lower frequency.
• Shorter wavelength means higher frequency.

Wavelength and frequency carry the same information — two ways to describe the same wave.

6–7 min. “Double the wavelength means half the frequency.”

Quick Check: Wavelength and Frequency

If one type of light has twice the wavelength of another, it has:

• Twice the frequency
• Half the frequency
• The same frequency
• Four times the frequency

1 min. Poll.

The Electromagnetic Spectrum

More than meets the eye

Visible Light Is a Tiny Sliver

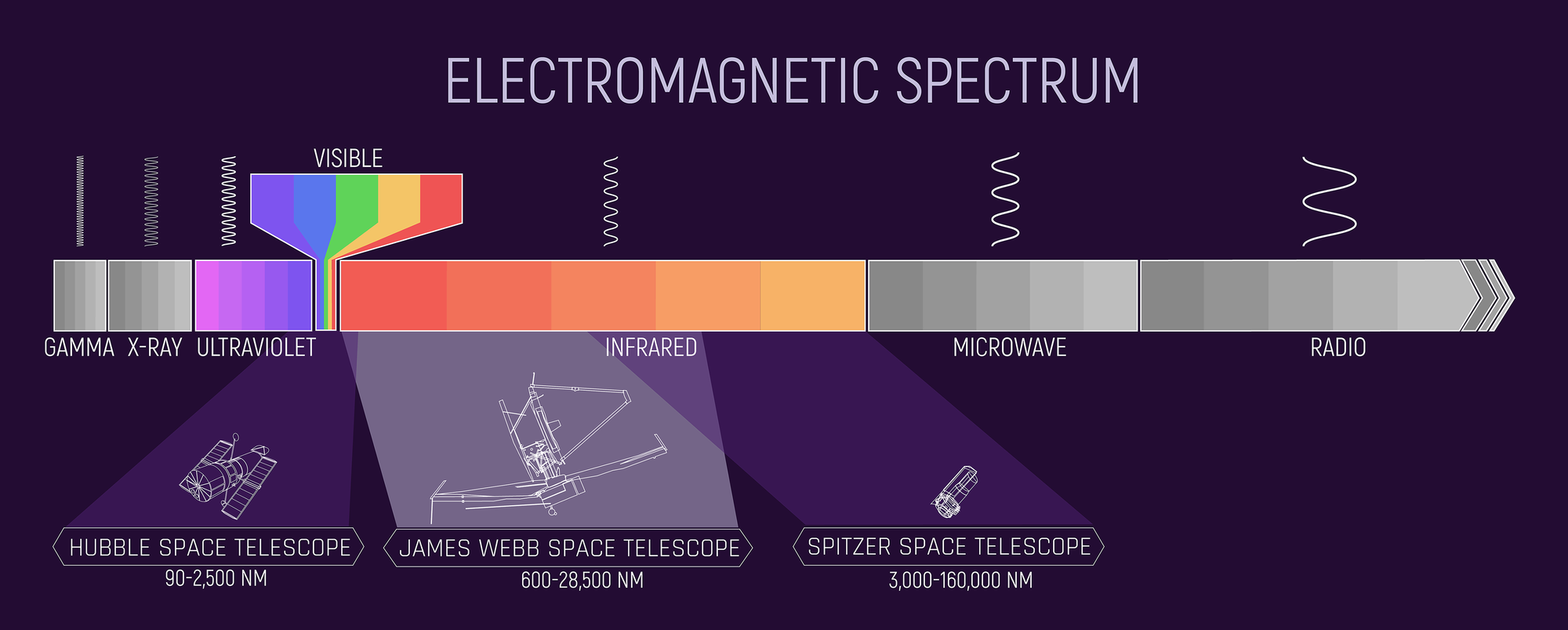
“Visible light” — the colors we see — is just a tiny fraction of the full spectrum.

7–8 min. “Radio to gamma rays — all are light. All travel at speed c.”

Full Electromagnetic Spectrum

Credit: Illustration: NASA, ESA, CSA

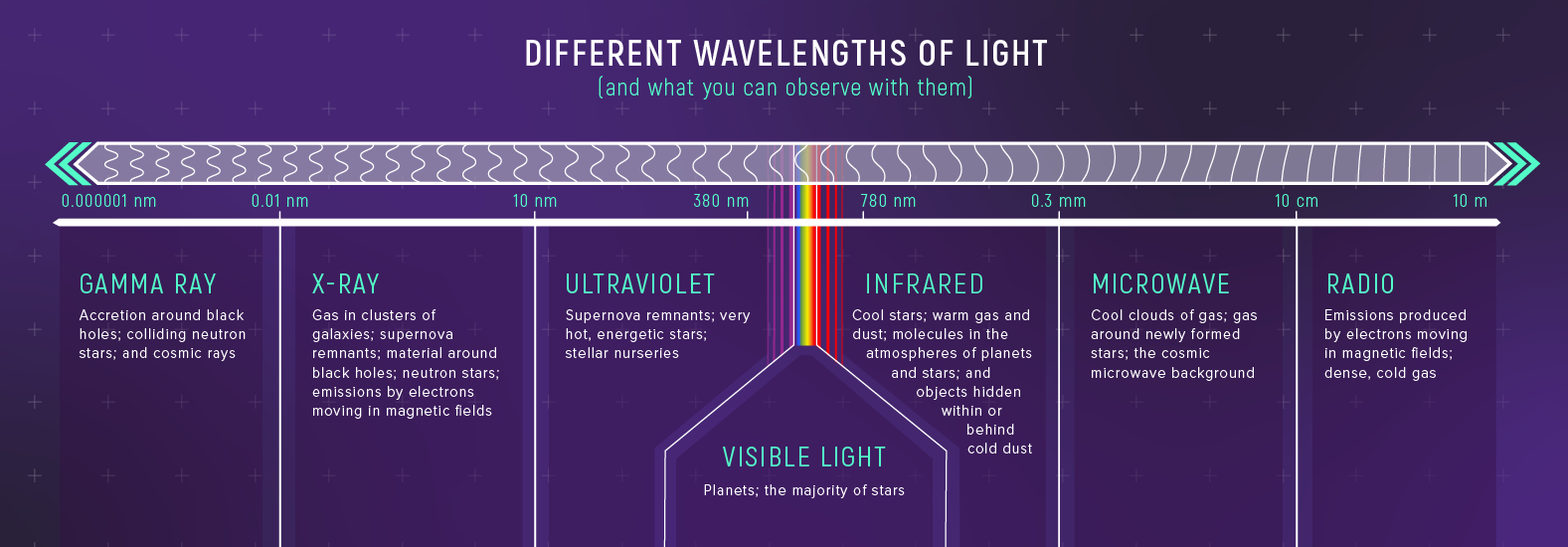
Visible light is only a narrow window in a much larger spectrum. Different wavelength bands trace different physics.

Point to visible as context, then move on quickly.

Spectrum Through Earth’s Atmosphere

Credit: NASA

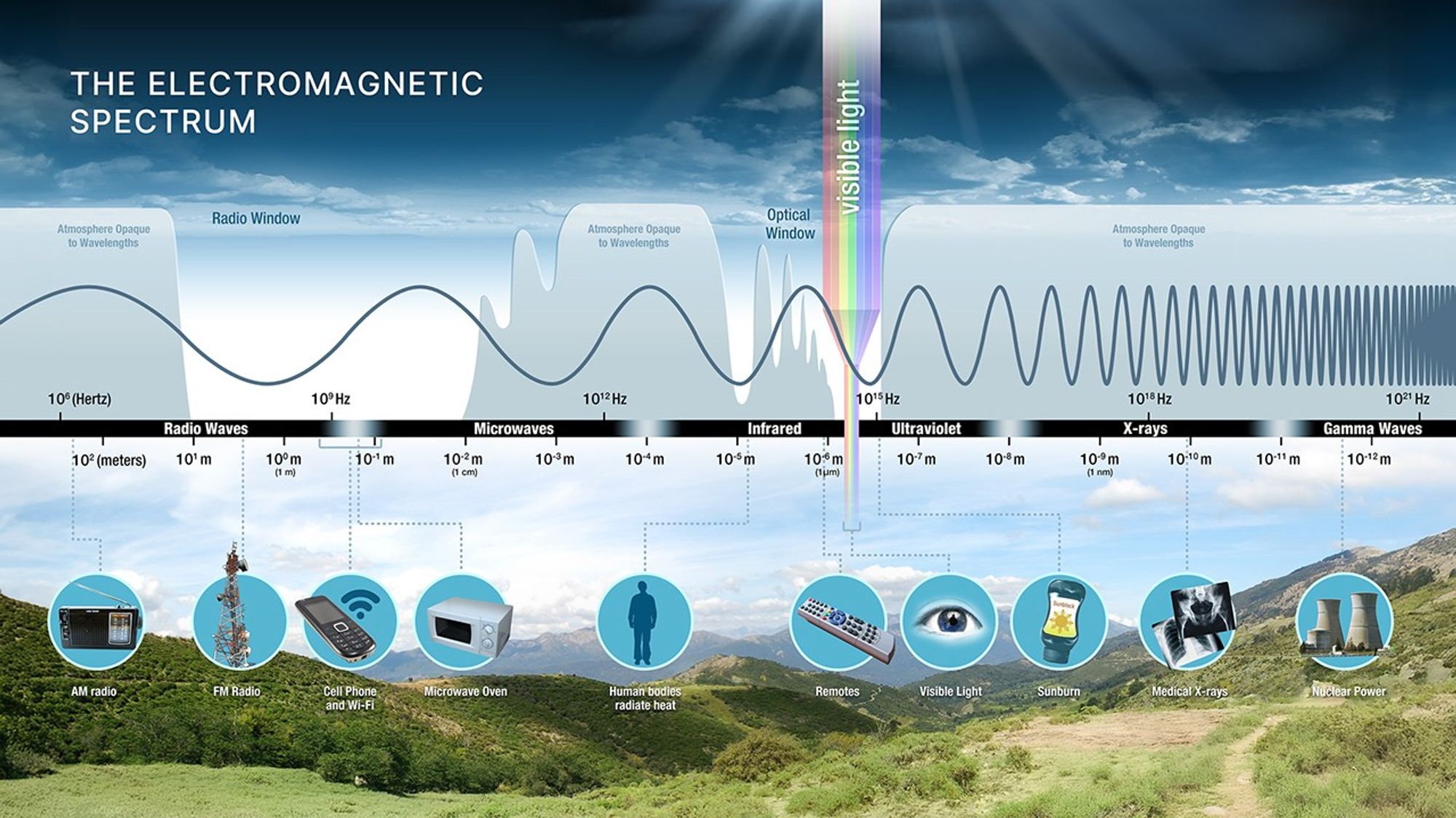
Radio and optical windows reach the ground; many other wavelengths require space telescopes.

Atmospheric transmission determines which observatories must be in space.

8 min. Reinforce why astronomy uses multiple telescope platforms.

The Full Spectrum (1/2)

Region	Wavelength	Astronomical uses
Radio	> 10 cm	Mapping hydrogen, pulsars
Microwave	1 mm – 10 cm	CMB, cold dust
Infrared	700 nm – 1 mm	Dust, cool stars
Visible	400 – 700 nm	Direct imaging

8–9 min. “Different wavelengths reveal different physics.”

The Full Spectrum (2/2)

Region	Wavelength	Astronomical uses
Ultraviolet	10 – 400 nm	Hot gas
X-ray	0.01 – 10 nm	Black holes, neutron stars
Gamma ray	< 0.01 nm	Supernovae, gamma-ray bursts

8–9 min. “Different wavelengths reveal different physics.”

How Light Interacts with Matter

Credit: Illustration: NASA, ESA, CSA

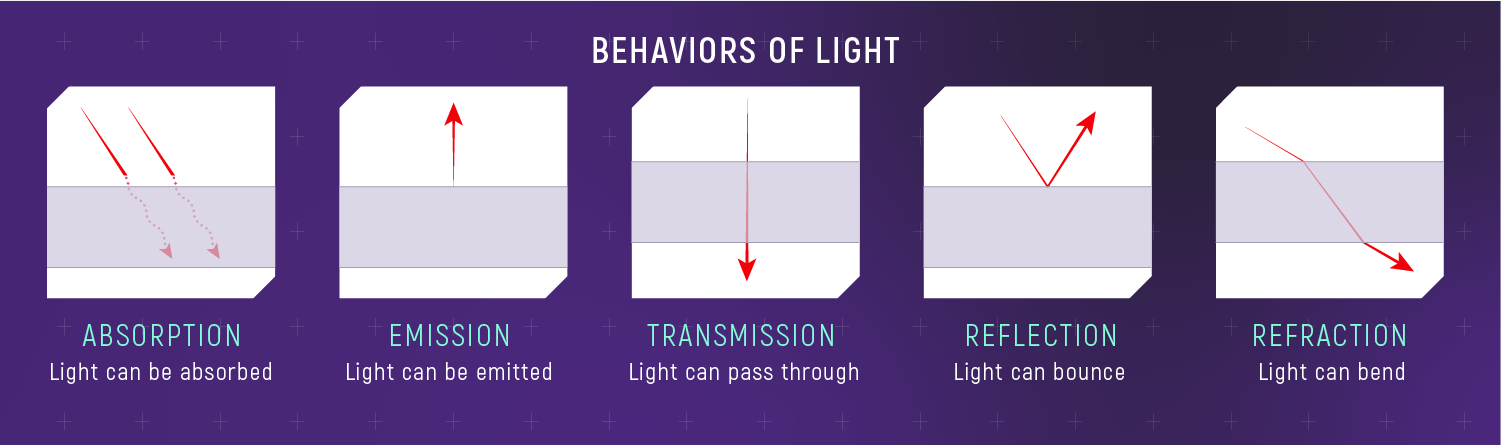
• Absorption removes specific wavelengths.
• Emission adds specific wavelengths.
• Reflection, refraction, and transmission change light paths.

8–9 min. Use this as the bridge from spectrum bands to measurable signatures.

Three Spectra Astronomers Use

Credit: Illustration: NASA, ESA, CSA

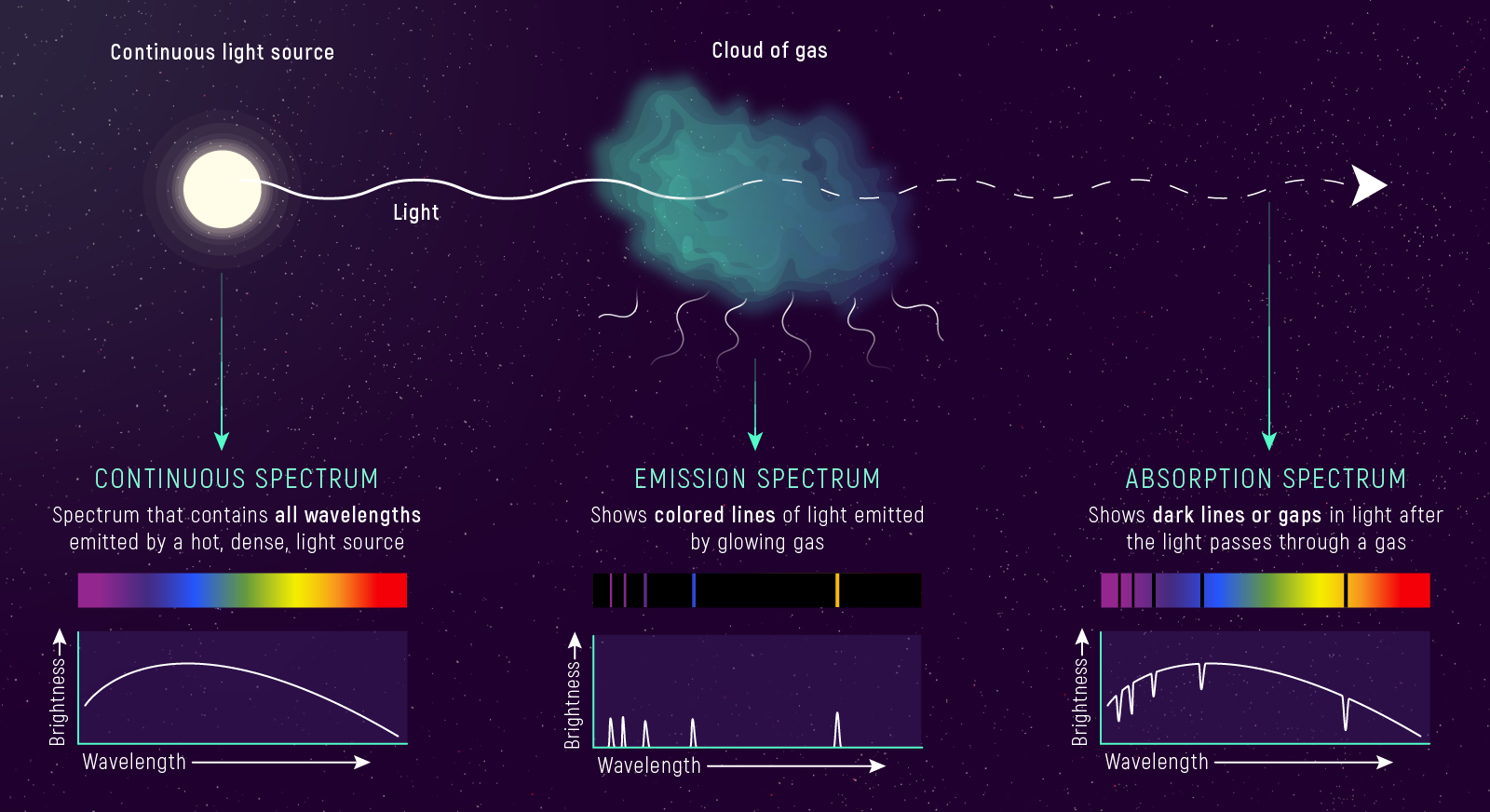
• Continuous: dense, hot source.
• Emission-line: hot, thin gas.
• Absorption-line: continuum through cooler gas.

9 min. This replaces the table with image-first interpretation.

Absorption and Emission Fingerprints

Credit: Illustration: NASA, ESA, CSA

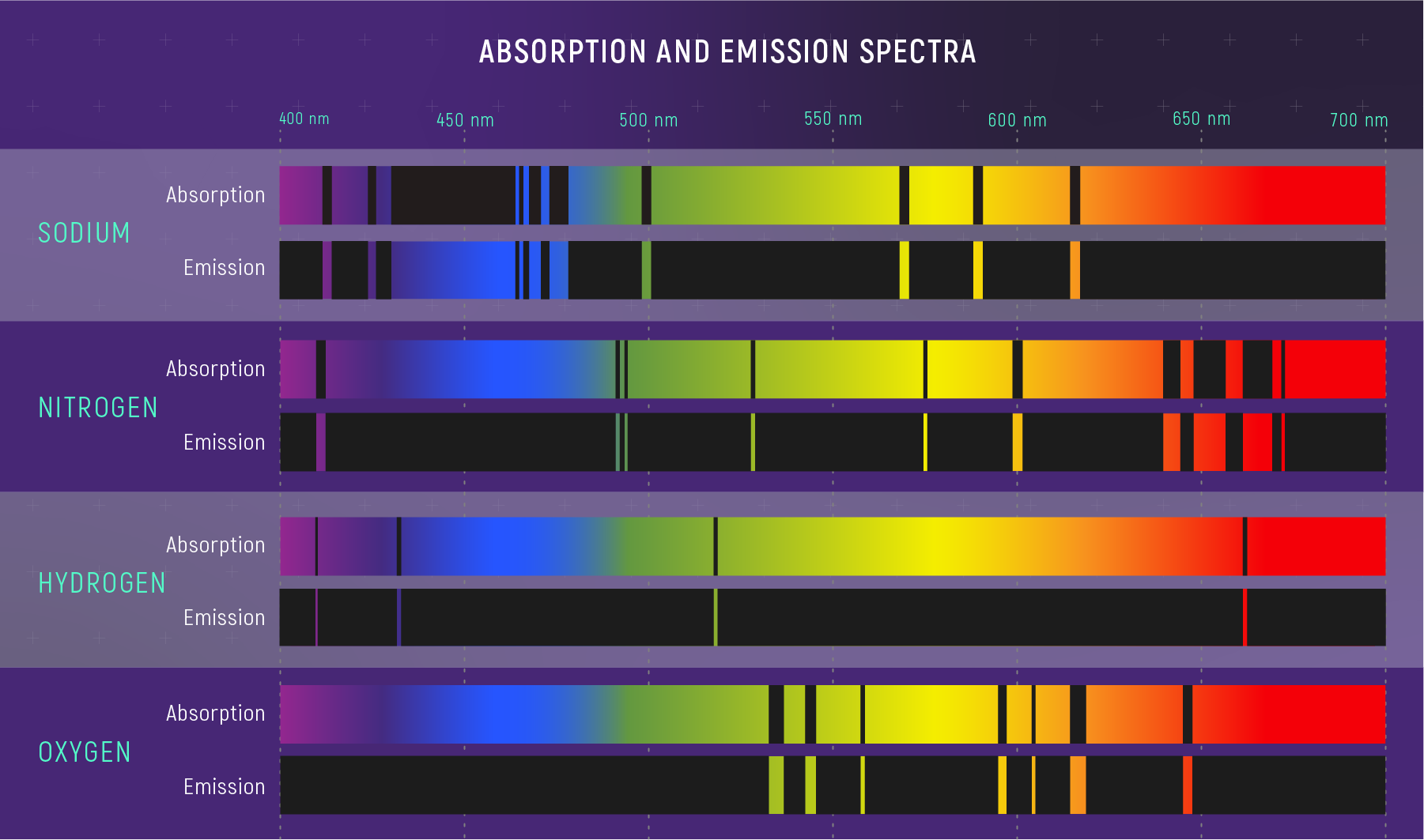
• Same element means the same line wavelengths.
• Absorption lines are dark where photons are removed.
• Emission lines are bright where photons are added.

9–10 min. Set up Lecture 8/9 spectroscopy logic with a concrete visual.

EM Spectrum in Astronomy

Credit: Illustration: NASA, ESA, CSA

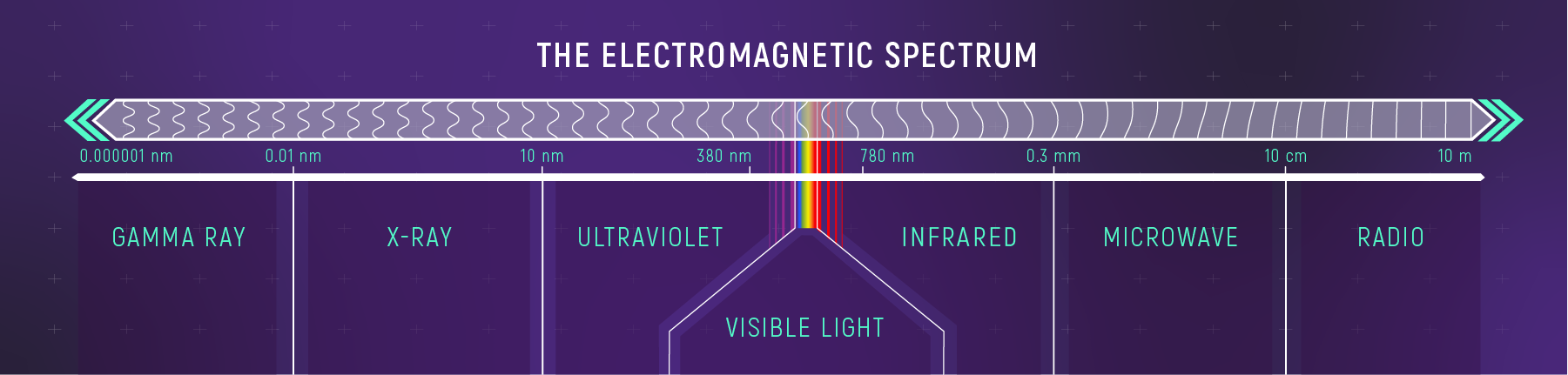
Different wavelength bands map to different physical regimes.

This complements the table with an image-first view.

Same Object, Different Wavelengths

The universe looks different at every wavelength.

9–10 min. “This is why astronomers build different types of telescopes.”

Crab Nebula Across Wavelengths

Credit: NASA/CXC/SAO

One object, multiple observables, multiple physical inferences.

Connect directly to “same object, different wavelength” claim.

Quick Check: Ordering the Spectrum

Which correctly orders these from longest to shortest wavelength?

• Gamma rays, X-rays, UV, Visible, Infrared, Radio
• Radio, Infrared, Visible, UV, X-rays, Gamma rays
• Visible, UV, Infrared, Radio, X-rays, Gamma rays
• Microwave, Radio, Visible, Infrared, Gamma rays

1 min. Poll.

Quick Check: Multiwavelength Astronomy

Why do astronomers observe the same object at different wavelengths?

• Different telescopes are in different locations
• Different wavelengths reveal different physical processes
• It’s cheaper to use old telescopes
• Visible light is too faint

1 min. Poll.

The Speed of Light

\(c = 299,792,458\) m/s

~300,000 km/s

This is the cosmic speed limit.

Nothing with mass can reach it.

And because light has finite speed…

looking out in space is looking back in time.

10–11 min. “The farther we see, the younger the universe appears.”

Light-Travel Time (1/2)

Object	Distance	Light-travel time
Moon	384,000 km	1.3 s
Sun	150 million km	8 min
Proxima Centauri	4.2 light-years	4.2 yr

11–12 min. Build intuition: nearby objects are minutes-to-years.

Light-Travel Time (2/2)

Object	Distance	Light-travel time
Andromeda Galaxy	2.5 million light-years	2.5 million yr
Distant galaxies	Billions of light-years	Billions of yr

When we observe the most distant galaxies, we’re seeing the early universe directly.

11–12 min. “The farther we look, the farther back in time we see.”

Quick Check: Light Travel Time

When we observe the Andromeda Galaxy (2.5 million light-years away), we see it as it was:

• Right now, in real time
• 2.5 years ago
• 2.5 million years ago
• Billions of years ago

1 min. Poll.

Part 2: Why Is the Sky Blue?

Rayleigh scattering

Sunlight Is All Colors

Credit: Illustration: NASA, ESA, CSA

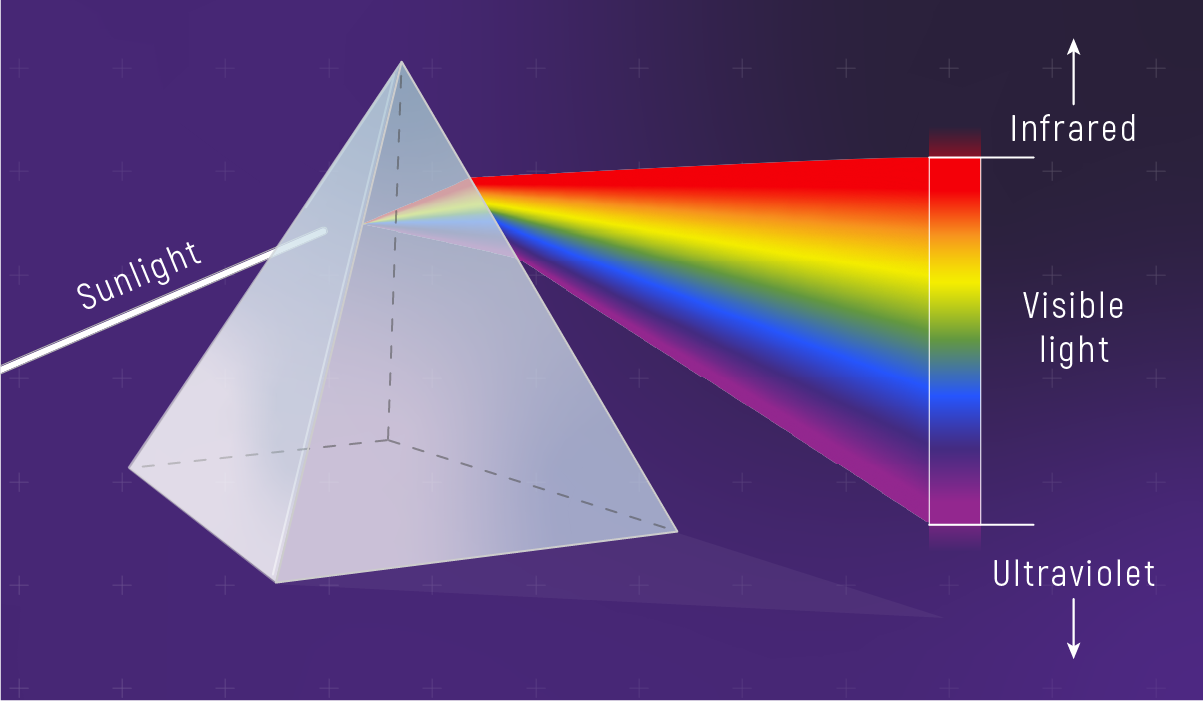
Sunlight is white light — a mix of all visible wavelengths.

So why does the sky favor blue?

12–13 min. “If sunlight has all colors, why is the sky blue?”

Rayleigh Scattering

\[\text{Scattering} \propto \frac{1}{\lambda^4}\]

Shorter wavelengths scatter MUCH more.

Valid when the scatterers are much smaller than the wavelength (e.g., atmospheric molecules).

Comparing blue (\(\lambda \approx 450\) nm) and red (\(\lambda \approx 700\) nm):

\[\left(\frac{700}{450}\right)^4 \approx 6\]

Blue scatters about \(6\times\) more than red!

13–14 min. “The \(1/\lambda^4\) makes a huge difference.”

Why the Sky Is Blue and Sunsets Are Red

Credit: (A. Rosen/NotebookLM)

Sky is blue: blue photons scatter in many directions, so they reach your eyes from across the sky.

Sunsets are red: along a longer atmospheric path, blue is scattered away and red/orange light remains.

14–16 min. Same physics, different geometry and line-of-sight path length.

Rayleigh Scattering in Real Sky Data

Credit: Gemini Observatory

The same wavelength-dependent scattering shows up in real atmospheric observations.

16 min. Tie model diagram to observed sky behavior.

Quick Check: Rayleigh Scattering

Blue light scatters more than red light because:

• Blue light is faster than red light
• Shorter wavelengths scatter more in Rayleigh scattering (\(\propto 1/\lambda^4\))
• Air molecules are blue
• The Sun emits more blue light

1 min. Poll.

Quick Check: Sunsets

Sunsets appear red because:

• The Sun turns red as it sets
• The atmosphere filters out red light, leaving blue
• Blue light has been scattered away on the long path through atmosphere
• Dust particles block the blue

1 min. Poll.

The Blood Moon

Same physics, cosmic scale

Lunar Eclipse Puzzle

During a total lunar eclipse, the Moon doesn’t go dark — it turns deep red.

Why doesn’t it go completely dark?

The Moon is in Earth’s shadow — no direct sunlight reaches it…

16–17 min. “Apply what you just learned about Rayleigh scattering!”

Earth’s Atmosphere as Filter

Credit: (A. Rosen/NotebookLM)

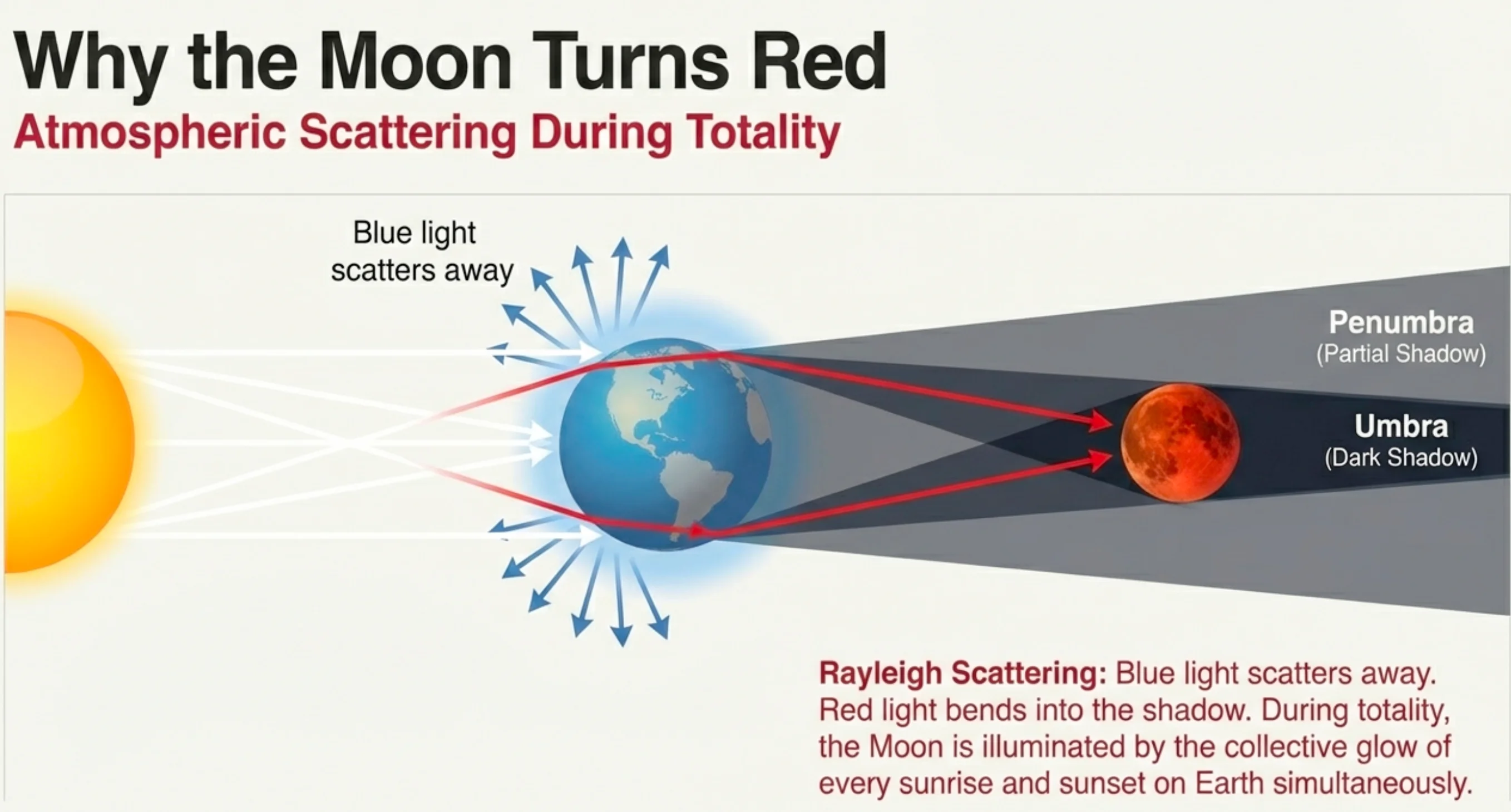
1. Sunlight passes through Earth’s atmosphere
2. Blue light scatters away (Rayleigh!)
3. Only red light makes it through
4. That red light bends toward the Moon

17–18 min. “It’s the light from every sunset on Earth, focused on the Moon.”

Quick Check: Blood Moon

During a total lunar eclipse, the Moon appears red because:

• The Moon reflects Mars’s light
• Earth’s atmosphere scatters blue away, letting red sunlight reach the Moon
• The Moon’s surface is actually red
• The Sun becomes cooler during eclipses

1 min. Poll.

Part 3: Light Intensity

Another inverse-square law

Inverse-Square Law for Light

\[I \propto \frac{1}{r^2}\]

Double your distance, receive 1/4 the intensity

Why? Light spreads over spheres.

Sphere area \(= 4\pi r^2\), so intensity drops as \(1/r^2\).

Same geometric argument as gravity (L6)!

18–19 min. “Same spreading-over-spheres argument as gravity.”

Credit: (A. Rosen/Gemini)

19–20 min. Visual of inverse-square spreading.

Distance and Brightness

Distance Change	Intensity Change
\(2\times\) farther	1/4 as bright
\(3\times\) farther	1/9 as bright
\(10\times\) farther	1/100 as bright
\(100\times\) farther	1/10,000 as bright

If we know true luminosity and measure apparent brightness, we can calculate distance!

20–21 min. “This is the foundation of distance measurement in astronomy.”

Quick Check: Distance and Brightness

A star appears 16 times fainter than an identical star nearby. How much farther away is the faint star?

• \(4\times\) farther
• \(16\times\) farther
• \(8\times\) farther
• \(2\times\) farther

1–2 min. Poll, then explain. Reasoning: \(I \propto 1/r^2\). If \(I = 1/16\), then \(r = 4\).

Quick Check: Two Stars

Star A is \(5\times\) farther away than Star B. If they have the same luminosity, Star A appears:

• \(5\times\) fainter
• \(10\times\) fainter
• \(25\times\) fainter
• \(125\times\) fainter

1–2 min. Poll, then explain. Reasoning: distance increases by \(5\), so intensity drops by \(5^2 = 25\).

Key Takeaways (1/2)

1. Light is an electromagnetic wave: \(c = \lambda \nu\).

2. The EM spectrum spans radio to gamma rays.

3. Rayleigh scattering: shorter wavelengths scatter more (\(\propto 1/\lambda^4\)).

4. Light intensity follows the inverse-square law: \(I \propto 1/r^2\).

21–23 min. Rapid recap.

Key Takeaways (2/2)

5. Blue sky and red sunsets are the same scattering physics.

6. Lunar eclipses are red for the same reason (sunset light).

7. Light is the astronomer’s primary tool: temperature, composition, motion, distance.

The Course Connection

L5-L6: Motion reveals mass

L7-L8: Light reveals temperature

L9: Spectral lines reveal composition and motion

Together: We can measure a star’s temperature, mass, composition, and velocity — all without touching anything.

23–24 min. “The astronomer’s toolkit.”

Coming Up: Temperature from Light

Next lecture: Everything glows.

Hotter objects glow bluer and brighter.

By analyzing the spectrum, we can read an object’s temperature from billions of kilometers away.

Reading: Lecture 8 Reading Companion

Demo: Explore the EM Spectrum: ../../../demos/em-spectrum/

24–25 min. Preview blackbody radiation.

Numerical Verification

Checking the wave equation and scattering

Let’s verify our equations with explicit calculations.

Verifying \(c = \lambda \nu\)

Given: Red light has wavelength \(\lambda = 700\) nm. What’s its frequency?

Step 1: Convert wavelength to meters

\[\lambda = 700 \text{ nm} \times \frac{10^{-9} \text{ m}}{1 \text{ nm}} = 7.00 \times 10^{-7} \text{ m}\]

Step 2: Solve for frequency

\[\nu = \frac{c}{\lambda} = \frac{3.00 \times 10^8 \text{ m/s}}{7.00 \times 10^{-7} \text{ m}}\]

\[\nu = 4.29 \times 10^{14} \text{ Hz} = 4.29 \times 10^{14} \text{ s}^{-1}\]

Unit check: \(\frac{\text{m/s}}{\text{m}} = \frac{1}{\text{s}} = \text{Hz}\)

“Red light oscillates 429 trillion times per second. That’s what frequency means.”

Frequency Comparison Across the Spectrum

Type	Wavelength	Frequency	Calculation
Radio (FM)	3 m	\(10^8\) Hz	\(\frac{3 \times 10^8}{3} = 10^8\)
Microwave	1 cm	\(3 \times 10^{10}\) Hz	\(\frac{3 \times 10^8}{10^{-2}}\)
Red light	700 nm	\(4.3 \times 10^{14}\) Hz	\(\frac{3 \times 10^8}{7 \times 10^{-7}}\)
Blue light	450 nm	\(6.7 \times 10^{14}\) Hz	\(\frac{3 \times 10^8}{4.5 \times 10^{-7}}\)
X-ray	1 nm	\(3 \times 10^{17}\) Hz	\(\frac{3 \times 10^8}{10^{-9}}\)

Pattern: Shorter wavelength means higher frequency (always!).

“The relationship is inverse. As \(\lambda\) decreases, \(\nu\) increases proportionally.”

Rayleigh Scattering: Full Calculation

How much more does blue scatter than red?

Blue: \(\lambda_b = 450\) nm, Red: \(\lambda_r = 700\) nm

Scattering ratio:

\[\frac{\text{Scattering}_{\text{blue}}}{\text{Scattering}_{\text{red}}} = \frac{1/\lambda_b^4}{1/\lambda_r^4} = \left(\frac{\lambda_r}{\lambda_b}\right)^4\]

\[= \left(\frac{700 \text{ nm}}{450 \text{ nm}}\right)^4 = (1.556)^4\]

\[= 5.86 \approx 6\]

Blue light scatters about \(6\times\) more than red light.

Units cancel: \((\text{nm}/\text{nm})^4\) is dimensionless.

“The fourth power makes a huge difference. Even a modest wavelength ratio becomes significant.”

Why Not Violet?

Violet (\(\lambda \approx 400\) nm) scatters even MORE than blue:

\[\left(\frac{700}{400}\right)^4 = (1.75)^4 = 9.4\]

Violet scatters \(9\times\) more than red!

Bridge: physics says violet should dominate, but perception depends on the source and the detector.

Why Not Violet? (continued)

So why isn’t the sky violet?

1. The Sun emits less violet than blue.
2. Our eyes are less sensitive to violet.
3. Some violet is absorbed by ozone.

Result: We perceive the scattered light as blue, not violet.

Inverse-Square Law: Star Distance Problem

Problem: Star A appears \(100\times\) fainter than Star B. If they’re identical, how much farther is Star A?

From inverse-square law:

\[\frac{I_A}{I_B} = \frac{r_B^2}{r_A^2}\]

\[\frac{1}{100} = \frac{r_B^2}{r_A^2}\]

“Set up the ratio first. Stop here and check that the ratio direction matches intuition.”

Inverse-Square Law: Solving the Distance Ratio

Problem: Star A appears \(100\times\) fainter than Star B. If they’re identical, how much farther is Star A?

Solving for distance ratio:

\[\frac{r_A}{r_B} = \sqrt{100} = 10\]

Star A is \(10\times\) farther away.

Note: We don’t need absolute distances — just the ratio!

“This is how astronomers bootstrap the distance ladder. Compare identical objects at different distances.”

Light Travel Time: Proxima Centauri

Given: Proxima Centauri is 4.24 light-years away. Express this in km.

Step 1: How far does light travel in 1 year?

\[d_{1\text{yr}} = c \times t = (3.00 \times 10^5 \text{ km/s}) \times (1 \text{ year})\]

Convert 1 year to seconds:

\[1 \text{ yr} = 365.25 \text{ days} \times 24 \text{ hr/day} \times 3600 \text{ s/hr} = 3.156 \times 10^7 \text{ s}\]

\[d_{1\text{ly}} = 3.00 \times 10^5 \times 3.156 \times 10^7 = 9.47 \times 10^{12} \text{ km}\]

Distance to Proxima Centauri:

\[d = 4.24 \times 9.47 \times 10^{12} \text{ km} = 4.01 \times 10^{13} \text{ km}\]

“40 trillion km to the nearest star. Space is incomprehensibly vast.”

Photon Energy

The quantum nature of light — essential foundation for Lectures 8 and 9

This section is NOT optional — photon energy (\(E = hc/\lambda\)) is required for understanding blackbody radiation (L8) and spectral lines (L9). Cover it fully.

Wavelength and Photon Energy

Credit: Illustration: NASA, ESA, CSA

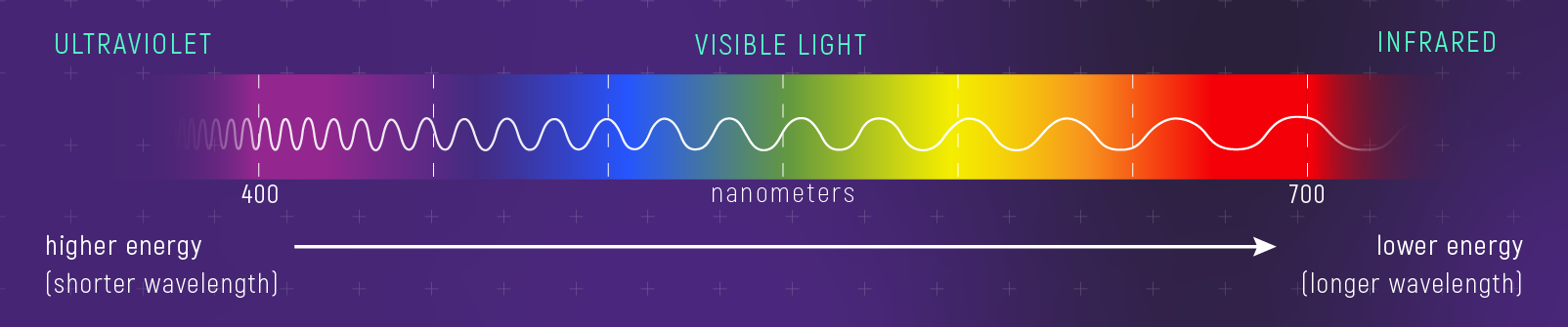
Shorter wavelength means higher photon energy.

Use as a visual bridge before writing \(E = h\nu\).

Light as Particles: Photons

Light behaves as both a wave and a particle.

Each particle of light — a photon — carries energy:

\[E = h\nu = \frac{hc}{\lambda}\]

Where:

• \(h = 6.626 \times 10^{-34}\ \mathrm{J\,s}\) (Planck’s constant)
• \(c = 3.00 \times 10^8\ \mathrm{m/s}\)
• \(hc = 1.986 \times 10^{-25}\ \mathrm{J\,m}\)

“This quantum nature of light is what we’ll need to understand spectral lines in L9.”

Photon Energy: Useful Forms

In Joules (SI units):

\[E = \frac{1.986 \times 10^{-25}\ \mathrm{J\,m}}{\lambda\ \text{(in meters)}}\]

In electron-volts (more convenient for atoms):

\[E = \frac{1240\ \mathrm{eV\,nm}}{\lambda\ \text{(in nm)}}\]

Example: Red photon (\(\lambda = 620\) nm)

\[E = \frac{1240\ \mathrm{eV\,nm}}{620\ \text{nm}} = 2.0\ \text{eV}\]

“The \(1240\ \mathrm{eV\,nm}\) is a convenient number to memorize. It comes from \(hc\) in these units.”

Where Does \(1240\ \mathrm{eV\,nm}\) Come From?

\[hc = (6.626 \times 10^{-34}\ \mathrm{J\,s}) \times (3.00 \times 10^8\ \mathrm{m/s})\]

\[= 1.988 \times 10^{-25}\ \mathrm{J\,m}\]

Convert J to eV:

\[1 \text{ eV} = 1.602 \times 10^{-19} \text{ J}\]

\[hc = \frac{1.988 \times 10^{-25}\ \mathrm{J\,m}}{1.602 \times 10^{-19}\ \mathrm{J/eV}} = 1.241 \times 10^{-6}\ \mathrm{eV\,m}\]

Convert m to nm:

\[hc = 1.241 \times 10^{-6}\ \mathrm{eV\,m} \times \frac{10^9\ \text{nm}}{1\ \text{m}} = 1241\ \mathrm{eV\,nm}\]

We round to \(1240\ \mathrm{eV\,nm}\) for convenience.

“I’m showing you the derivation so you understand where this number comes from. Always know your units!”

Photon Energies Across the Spectrum (1/2)

Light	Wavelength	Energy (eV)
Radio	1 m = \(10^9\) nm	\(1.24 \times 10^{-6}\)
Infrared	10,000 nm	0.124
Red	620 nm	2.0
Blue	450 nm	2.76

The conversion comes from \(E = hc/\lambda\) with the convenient form \(E(\text{eV}) \approx 1240/\lambda(\text{nm})\).

Photon Energies Across the Spectrum (2/2)

Light	Wavelength	Energy (eV)
UV	100 nm	12.4
X-ray	1 nm	1,240

Shorter wavelength means higher photon energy.

“This is why X-rays are dangerous and radio waves aren’t. It’s about energy per photon.”

Why UV Causes Sunburn

It’s not about intensity — it’s about energy per photon.

Shorter-wavelength photons carry more energy per photon.

UV photons can break chemical bonds (sunburn risk). Visible photons usually cannot.

This connects directly to \(E = hc/\lambda\): shorter wavelength means higher energy per photon.

Optional context (keep qualitative): UV-A is lower energy, UV-B causes sunburn, and UV-C is blocked by ozone.

Example intuition: you can sit under a bright red lamp with no damage, but UV can cause burns because the photons are higher energy.

Questions?

Light is the universe’s messenger.

Every photon carries information.

Remaining time for questions.