Reading the Glow

Temperature Written in Light

Dr. Anna Rosen

February 11, 2026

Everything glows.

You. Your laptop. The walls around you.

Most of it is infrared — invisible to your eyes.

But heat something up…

0–1 min. Let this sink in. “You’re glowing right now.”

Color tracks temperature

Heat it to \(500^{\circ}\mathrm{C}\) \(\to\) dull red

Heat it to \(1000^{\circ}\mathrm{C}\) \(\to\) bright orange

Heat it to 5800 K \(\to\) brilliant white

The color of the glow tells you the temperature.

1–2 min. “This is the astronomer’s thermometer.”

🖥️ Explore: Infrared Animals

~2 min. ViewSpace interactive (NASA/STScI). Drag the slider from VISIBLE to INFRARED.

• Animals that blend in visually (camouflage) still glow in infrared — they can’t hide their thermal radiation
• Cold-blooded vs warm-blooded: meerkats glow bright, the tomistoma (crocodile relative) is much dimmer
• Key connection: everything with temperature above absolute zero emits infrared — Wien’s Law in action

Ask: “Why does the crocodile almost disappear in infrared while the meerkats glow?” (Answer: Cold-blooded → lower body temperature → less thermal emission.)

Betelgeuse and Sirius are both among the brightest stars in the winter sky.

One is 880 times the Sun’s radius. The other is just 1.7×.

How could we possibly know that — without visiting either one?

By the end of today, you’ll be able to answer this.

~1 min. Let the mystery land. “This is today’s question. We’ll build the tools to solve it, one law at a time.”

Today’s Learning Objectives

By the end of today, you’ll be able to:

• Explain that all objects with temperature emit thermal radiation
• Define a blackbody and explain why stars approximate blackbodies
• Apply Wien’s Law to connect peak wavelength and temperature
• Explain why the Sun appears white even though its peak is green
• Apply the Stefan-Boltzmann Law to relate temperature and luminosity
• Connect luminosity, temperature, and radius: \(L = 4\pi R^2 \sigma T^4\)
• Use the ratio method to calculate stellar properties in solar units
• Infer stellar size when temperature is fixed but luminosity differs

2–3 min. “Today we learn to read temperature from light.”

Quick Review: The Kelvin Scale

In physics, we measure temperature in Kelvin — starts at absolute zero.

Landmark	Celsius	Kelvin
Absolute zero	\(-273^{\circ}\mathrm{C}\)	0 K
Room temperature	\(20^{\circ}\mathrm{C}\)	293 K
Sun’s surface	\(5500^{\circ}\mathrm{C}\)	5800 K

Quick rule: \(T_K = T_C + 273\)

“Double the temperature” only makes physical sense in Kelvin.

~1 min. Many gen-ed students have never used Kelvin. Quick orientation before equations.

Part 1: Everything Glows

Thermal radiation

Thermal Radiation

All objects with temperature above absolute zero emit electromagnetic radiation.

This is thermal radiation — comes from thermal motion of particles.

No external source needed — the object emits because it has internal energy.

3–4 min. “Even you, at ~310 K, emit ~100 W of infrared light.”

Examples Across Temperatures

Object	Temperature	Peak Wavelength	Emission
Cosmic background	2.7 K	~1 mm	Microwaves
Room temperature	300 K	~\(10\,\mu\mathrm{m}\)	Infrared
Red-hot metal	~1000 K	~\(3\,\mu\mathrm{m}\)	Near-IR, dull red
Sun’s surface	5800 K	~500 nm	Visible (green peak)
Hot blue star	30,000 K	~100 nm	Ultraviolet

Pattern: hotter \(\to\) shorter wavelength

4–5 min. “Cool objects emit infrared. Hot objects emit visible and UV.”

Quick Check: Thermal Radiation

Which of the following emits thermal radiation?

• Only the Sun and stars
• Only objects that are visibly glowing
• Everything with temperature above absolute zero
• Only objects connected to power sources

1 min. Poll.

What Is a Blackbody?

A blackbody is an idealized object with two properties:

1. It absorbs all incident radiation — nothing reflected
2. It emits thermal radiation with a spectrum determined only by temperature

Temperature alone determines the spectrum.

A blackbody iron ball at 5800 K emits the same spectrum as a blackbody tungsten ball at 5800 K — or the Sun.

5–6 min. “The spectrum is universal — depends only on T.”

Quick Recall: Photon Energy (Lecture 7)

Each photon carries energy:

\[E = h\nu = \frac{hc}{\lambda}\]

• \(h = 6.626 \times 10^{-34}\ \mathrm{J \cdot s}\) (Planck’s constant)
• \(\nu\) = frequency (Hz), \(\lambda\) = wavelength (m), linked by \(c = \lambda\nu\)
• Shortcut: \(E\ (\mathrm{eV}) \approx 1240 / \lambda\ (\mathrm{nm})\)

Shorter wavelength → higher energy per photon

(high energy) Gamma → X-ray → UV → Visible → IR → Radio (low energy)

Predict: Hotter objects peak at shorter \(\lambda\) — do they emit more energetic photons?

~1 min. Recall from L7 Part 6. Walk through the equation with units: \(E = hc/\lambda\), so if \(\lambda\) halves, \(E\) doubles. The key bridge: hotter blackbodies peak at shorter wavelengths (Wien’s Law) AND emit more energetic photons. Students should predict “yes” before you show the blackbody curves.

The Blackbody Spectrum

Credit: Illustration: NASA, ESA, CSA

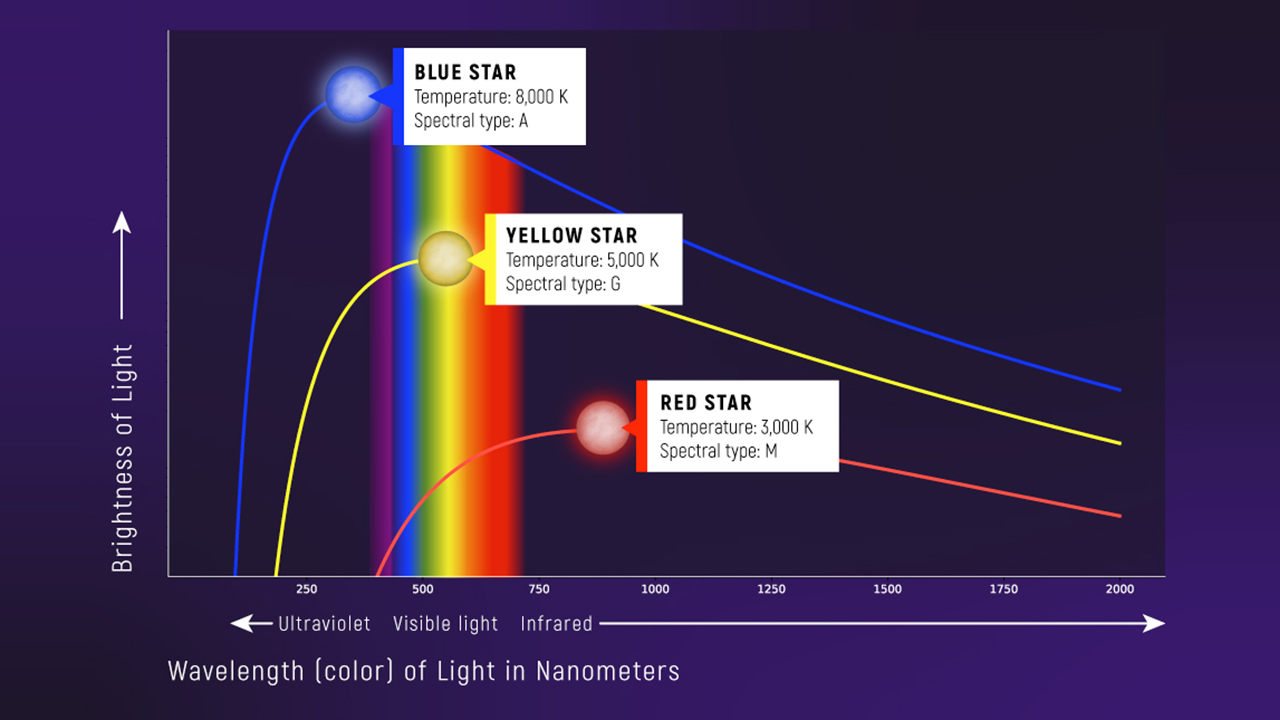
• Hotter \(\to\) peak shifts to shorter wavelengths (bluer)
• Hotter \(\to\) curve is taller (more total energy)

Both Wien’s Law and Stefan-Boltzmann are visible in these curves.

6–7 min. “Two effects: peak shifts AND total energy increases.” The two-column layout lets students study the curves while reading the key takeaways.

Why Stars Are (Nearly) Blackbodies

Credit: NASA/SDO

1. Stars are opaque — photons interact many times before escaping
2. Those interactions thermalize the radiation
3. The light we see comes from the photosphere — characterized by temperature

Real stellar spectra have spectral lines on top of the blackbody continuum — we’ll use those in Lecture 9.

7–8 min. “Stars approximate blackbodies for the smooth continuum.” SDO image shows the Sun’s photosphere glowing at ~5800 K.

Quick Check: Blackbody Concept

A blackbody’s emission spectrum depends on:

• What the object is made of
• The object’s color and reflectivity
• Only the object’s temperature
• The type of EM wave hitting it

1 min. Poll.

Part 2: Wien’s Law

Temperature from color

Predict First!

If you double an object’s temperature (in Kelvin), its peak wavelength…

1. Doubles

2. Stays the same

3. Halves

4. Drops to 1/4

30 sec. Have students vote before revealing.

Wien’s Displacement Law

\[\lambda_{\text{peak}} = \frac{2.9 \times 10^6\,\mathrm{nm\cdot K}}{T\,(\mathrm{K})}\]

Hotter objects peak at shorter wavelengths.

This is the astronomer’s thermometer:

Measure peak wavelength \(\to\) know the temperature.

8–9 min. “Wien’s Law lets us measure stellar temperatures remotely.”

Wien’s Law in Action

Object	Temperature	Peak Wavelength	Where
Cool red star	3000 K	~970 nm	Near-infrared
Sun	5800 K	~500 nm	Green visible
Hot white star	10,000 K	~290 nm	Ultraviolet
Hot blue star	25,000 K	~120 nm	Far ultraviolet

9–10 min. “Hotter stars peak at shorter wavelengths.”

Worked Example

Problem: A star’s spectrum peaks at 290 nm (UV). What is its temperature?

\[T = \frac{2.9 \times 10^6\,\mathrm{nm\cdot K}}{290\,\mathrm{nm}} = 10^4\,\mathrm{K}\]

This is a hot, blue-white star — about \(1.7\times\) the Sun’s temperature.

10–11 min. Walk through the calculation.

Quick Check: Wien’s Law

A cool red star has a surface temperature of 3000 K. Where does its spectrum peak?

• 100 nm (ultraviolet)
• 500 nm (visible green)
• 970 nm (near-infrared)
• 10,000 nm (far infrared)

1–2 min. Poll, then explain.

Calculation: \(\lambda = 2.9 \times 10^6\,\mathrm{nm\cdot K}\, / \, 3000\,\mathrm{K} = 967\,\mathrm{nm} \approx 970\,\mathrm{nm}\) (near-IR).

🖥️ Live Demo: Blackbody Radiation

~3 min. Live demo. Adjust the temperature slider:

1. Start at ~5800 K (Sun) — note peak at green (~500 nm)
2. Drop to ~3000 K (red star) — peak shifts to infrared
3. Raise to ~10,000 K — peak shifts to UV
4. Point out: the curve gets TALLER and shifts LEFT as T rises — two effects at once (Wien + Stefan-Boltzmann)

Ask students: “What color star would peak at 500 nm?” (Answer: the Sun!)

The “Sun Is Green” Puzzle

Plug in the Sun’s temperature (5800 K):

\[\lambda_{\text{peak}} = \frac{2.9 \times 10^6\,\mathrm{nm\cdot K}}{5800\,\mathrm{K}} = 500\,\mathrm{nm}\]

That’s green light!

Yet the Sun doesn’t look green…

11–12 min. “So why doesn’t the Sun look green?”

The Sun’s Spectrum Is Broad

Credit: Illustration: NASA, ESA, CSA

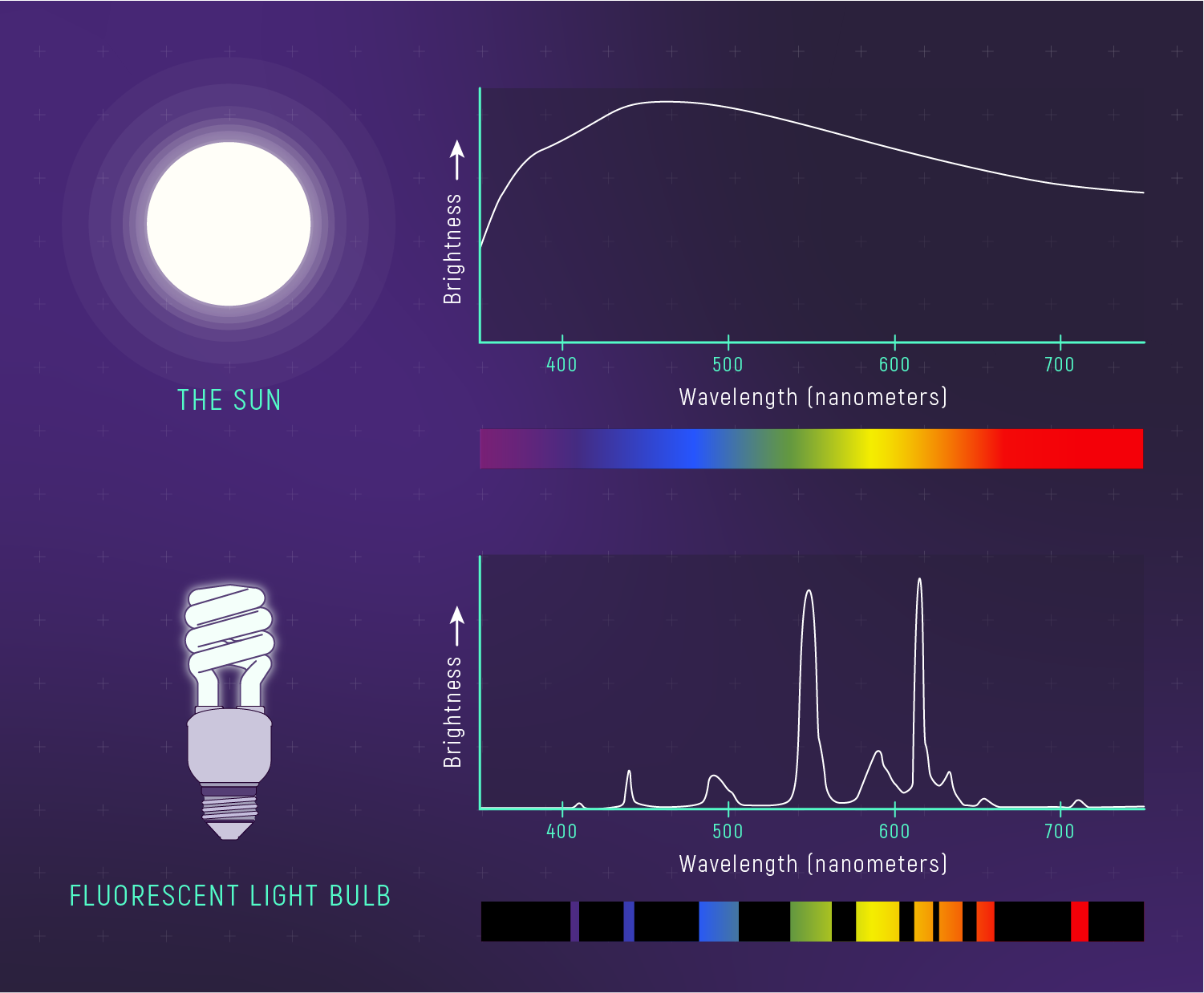
The peak is near green, but the curve spans the full visible band.

Use the figure to make the white-light explanation intuitive.

Why the Sun Isn’t Green

1. Blackbody curves are broad.

The Sun emits across ALL visible wavelengths — not just the peak.

2. Our eyes see the mix as white.

When all colors are present, we perceive white light.

If the Sun emitted ONLY at 500 nm, it would look green.

But blackbody spectra are continuous and broad.

12–13 min. “Broad spectrum \(\to\) white appearance.”

Quick Check: Why Not Green?

The Sun’s blackbody spectrum peaks at ~500 nm (green). Why doesn’t the Sun appear green?

• The Sun doesn’t actually emit green light
• Earth’s atmosphere absorbs all the green
• The Sun emits broadly across all visible wavelengths; we see white
• Our eyes can’t see green light

1 min. Poll.

Star Colors = Temperatures

Color	Temperature	Example Stars
Red/orange	3000–4500 K	Betelgeuse, Antares
Yellow	5000–6000 K	Sun, Alpha Centauri A
White	7000–10,000 K	Sirius A, Vega
Blue-white	10,000–30,000+ K	Rigel, Spica

Wien’s Law in action: color reveals temperature.

13–14 min. “No thermometer needed — just analyze the color.”

Star Colors in the Wild: NGC 6355

Credit: NASA, ESA, Hubble

In this Hubble image of globular cluster NGC 6355, each star’s color tells its temperature — Wien’s Law in one glance.

“Look at the range of colors — blue-white, yellow, orange, red. Each color is a temperature. This is Wien’s Law written across the sky.”

Quick Check: Star Colors

Rank these stars from coolest to hottest: Rigel (blue-white), Betelgeuse (red), Sun (yellow-white).

• Rigel, Sun, Betelgeuse
• Betelgeuse, Sun, Rigel
• Sun, Betelgeuse, Rigel
• They’re all the same temperature

1 min. Poll.

Observable → Model → Inference

The astronomer’s thermometer:

Observable: A star’s spectrum peaks at 580 nm (yellow-orange light).

Model: Wien’s Law — \(\lambda_{\text{peak}}\,(\mathrm{nm}) = 2.9 \times 10^6\,\mathrm{nm\cdot K}\, / \, T\,(\mathrm{K})\)

Inference: \(T = 2.9 \times 10^6\,\mathrm{nm\cdot K}\, / \, 580\,\mathrm{nm} = 5000\,\mathrm{K}\). Slightly cooler than the Sun.

No thermometer. No contact. Just light carrying information across the cosmos.

~1 min. Reinforce the O→M→I framework. This is the course throughline: L5-L6 (motion reveals mass), L7-L8 (light reveals temperature).

Part 3: Stefan-Boltzmann Law

Temperature and luminosity

Remember the Demo?

When you raised the temperature, two things happened:

1. The peak shifted left — that was Wien’s Law (Part 2)
2. The curve got much taller — that’s what we’ll quantify now

How much taller? The answer is dramatic.

~30 sec. Bridge from demo to Stefan-Boltzmann. Students have the visual memory of the curve growing — anchor the math to that.

Predict First!

If you double an object’s temperature, its total energy output…

1. Doubles

2. Quadruples

3. \(8\times\)

4. \(16\times\)

30 sec. Have students vote before revealing.

Stefan-Boltzmann Law

\[\text{Power per area} = \sigma T^4\]

Temperature has a HUGE effect on luminosity.

\(\sigma = 5.67 \times 10^{-8}\ \mathrm{W\,m^{-2}\,K^{-4}}\) (Stefan-Boltzmann constant). Use \(T\) in Kelvin.

The fourth power is dramatic:

Temperature Factor	Luminosity Factor
\(2\times\) hotter	\(2^4 = 16\times\) more luminous
\(3\times\) hotter	\(3^4 = 81\times\) more luminous
\(10\times\) hotter	\(10^4 = 10,000\times\) more luminous

14–15 min. “Temperature is the dominant factor in stellar luminosity.”

Quick Check: Stefan-Boltzmann

Star A has twice the surface temperature of Star B. If both have the same radius, Star A is:

• \(2\times\) more luminous
• \(4\times\) more luminous
• \(8\times\) more luminous
• \(16\times\) more luminous

1 min. Poll.

The L-T-R Connection

\[L = 4\pi R^2 \sigma T^4\]

Luminosity depends on both size (\(R^2\)) and temperature (\(T^4\)).

\(L\) = luminosity (W), \(R\) = radius (m), \(T\) = surface temperature (K), \(\sigma = 5.67 \times 10^{-8}\ \mathrm{W\,m^{-2}\,K^{-4}}\).

A star can be luminous because:

• It’s very hot (even if small)
• It’s very large (even if cool)
• Or both!

15–16 min. “This is how we distinguish giants from dwarfs.”

How Many Light Bulbs?

The Sun’s luminosity: \(L_\odot = 3.84 \times 10^{26}\) W

A typical LED bulb: 10 W

Number of bulbs to match the Sun:

\[N = \frac{3.84 \times 10^{26}\,\mathrm{W}}{10\,\mathrm{W}} = 3.84 \times 10^{25} \text{ bulbs}\]

That’s 38 trillion trillion LED bulbs!

Or about 5 billion bulbs for every human who has ever lived.

~1 min. “Just to give you a sense of scale — the Sun is absurdly powerful. And that’s just one star.”

The Pillars of Creation: Wien’s Law in Action

Credit: Illustration: NASA, ESA, CSA

Left: Hubble (visible) — Right: Webb (near-IR)

Credit: Illustration: NASA, ESA, CSA

• Glowing gas (~10,000 K) → peaks in visible
• Dust pillars (~20–50 K) → opaque here
• Newborn stars (~3,000 K) → peaks in near-IR

Wien’s Law told astronomers where to look. Stefan-Boltzmann told them what they’d find.

~1 min. The blackbody curves on the right show exactly where each component falls. The gas glows in visible because it’s ~10,000 K. The dust is cold (~20–50 K), peaks in far-IR, and blocks visible light. But Webb observes in near-infrared, where that dust becomes transparent — revealing thousands of newborn stars that Hubble could never see. “This is what the physics buys you.”

Same Temperature, Different Luminosity

Two stars at the same temperature but different luminosities…

must have different sizes.

If Star A and Star B have the same \(T\) but Star A is \(100\times\) more luminous…

Then Star A has \(10\times\) the radius (since \(L \propto R^2\)).

This is how we distinguish giants from dwarfs.

16–17 min. “Same color, different brightness \(\to\) different size.”

Credit: ESO/ALMA

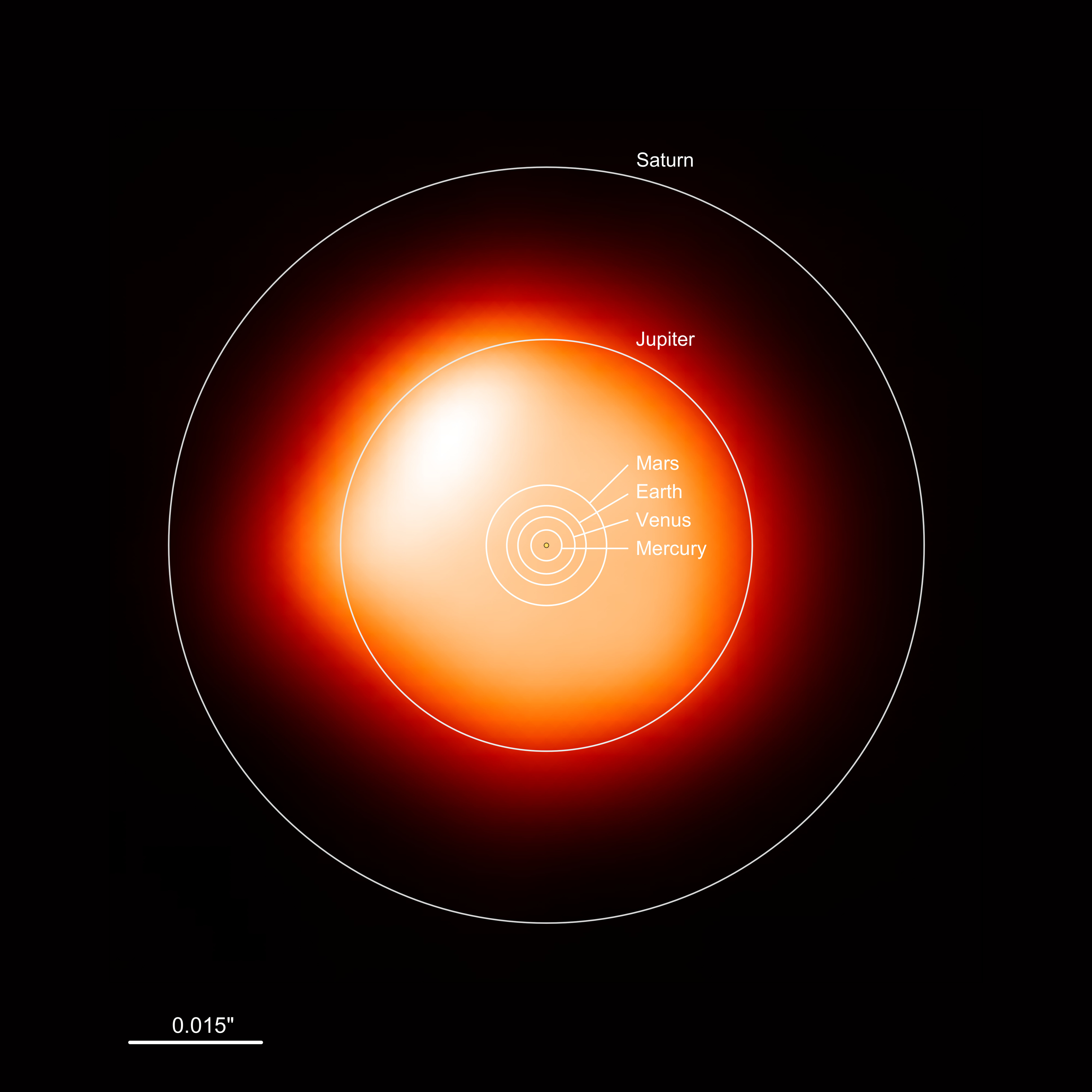
Betelgeuse is a red giant — same color as red dwarfs, but ~\(1000\times\) the radius.

17–18 min. “Same temperature, vastly different size.”

Preview: The H-R Diagram

Credit: ESO

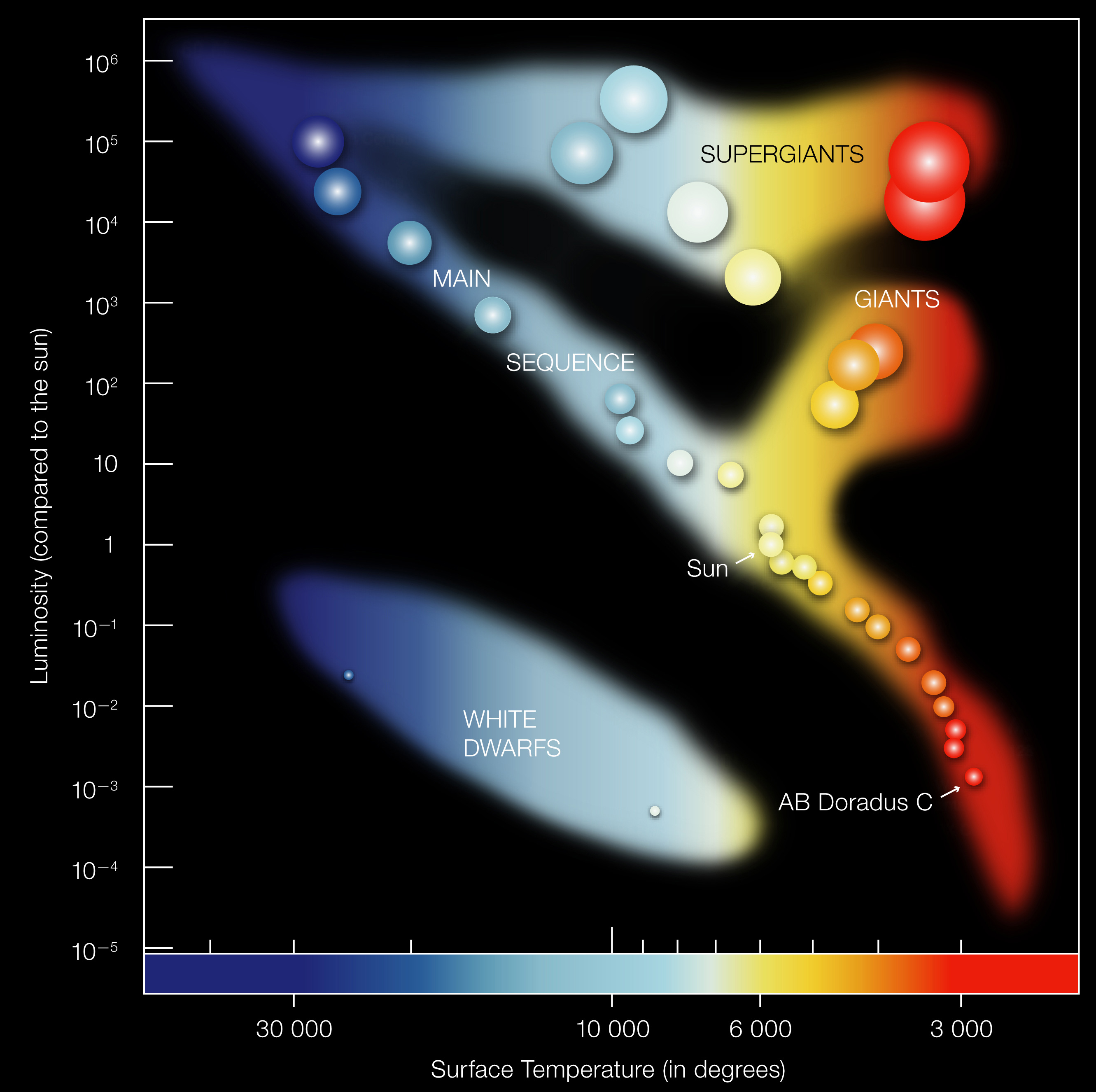
Temperature (\(x\)-axis) vs. luminosity (\(y\)-axis). The L-T-R relationship organizes all of stellar astrophysics.

~1 min. “We’ll study this diagram in detail in Module 2. For now, notice: same temperature but different luminosity means different size — that’s what we just learned.”

Worked Example

Problem: Two stars have the same temperature. Star A has \(100\times\) the luminosity of Star B. How do their radii compare?

Since \(L \propto R^2 T^4\) and \(T\) is the same:

\[\frac{R_A}{R_B} = \left(\frac{L_A}{L_B}\right)^{1/2} = 100^{1/2} = 10\]

Star A has \(10\times\) the radius of Star B.

18–19 min. Walk through the calculation.

Quick Check: Giants vs Dwarfs

A red giant and a red dwarf have the same surface temperature. The giant is \(10^4\) times more luminous. How do their radii compare?

• Giant’s radius is \(10\times\) the dwarf’s
• Giant’s radius is \(100\times\) the dwarf’s
• Giant’s radius is \(10^4\) times the dwarf’s
• Their radii are the same

1–2 min. Poll, then explain.

Solution: \(R_{\text{giant}}/R_{\text{dwarf}} = (10^4)^{1/2} = 10^2 = 100\).

Quick Check: L-T-R Synthesis

Star X is twice as hot as Star Y and has half the radius. How does Star X’s luminosity compare?

• Same luminosity
• \(2\times\) more luminous
• \(4\times\) more luminous
• \(8\times\) more luminous

1–2 min. Poll, then explain.

Solution: \(L_X/L_Y = (1/2)^2 \times (2)^4 = (1/4) \times 16 = 4\).

Part 4: The Astronomer’s Shortcut

Ratios and solar units

Working in Solar Units

The L-T-R equation has constants (\(4\pi\), \(\sigma\)) that are awkward to use. But there’s a trick:

Write the equation for any star:

\[L_{\star} = 4\pi R_{\star}^2 \sigma T_{\star}^4\]

Write the same equation for the Sun:

\[L_\odot = 4\pi R_\odot^2 \sigma T_\odot^4\]

Divide star by Sun — constants cancel!

\[\frac{L_{\star}}{L_\odot} = \left(\frac{R_{\star}}{R_\odot}\right)^2 \left(\frac{T_{\star}}{T_\odot}\right)^4\]

~2 min. “This is the ratio method — the astronomer’s shortcut. No constants needed, just compare to the Sun.”

Why This Works

\[\frac{L}{L_\odot} = \left(\frac{R}{R_\odot}\right)^2 \left(\frac{T}{T_\odot}\right)^4\]

What happened?

• \(4\pi\) canceled
• \(\sigma\) canceled
• We only need ratios — no SI units, no scientific notation!

This works because \(4\pi\) and \(\sigma\) are the same for every star. The physics is in the ratios.

“This is what professional astronomers actually use. Textbooks give you \(\sigma = 5.67 \times 10^{-8}\) — we almost never plug that in.”

Think-Pair-Share: Why does this trick work? What’s special about dividing one equation by the same equation for a different star? (Answer: same constants appear in both, so they cancel.)

Worked Example: Sirius A

Problem: Sirius A is \(25\times\) more luminous than the Sun and has \(T = 9940\,\mathrm{K}\) (\(T_\odot = 5800\,\mathrm{K}\)). What’s its radius?

\[\frac{L}{L_\odot} = 25 = \left(\frac{R}{R_\odot}\right)^2 \left(\frac{9940\,\mathrm{K}}{5800\,\mathrm{K}}\right)^4\]

\[25 = \left(\frac{R}{R_\odot}\right)^2 \times (1.71)^4 = \left(\frac{R}{R_\odot}\right)^2 \times 8.6\]

\[\left(\frac{R}{R_\odot}\right)^2 = \frac{25}{8.6} = 2.9 \quad \Rightarrow \quad \frac{R}{R_\odot} = 2.9^{1/2} = 1.7\]

Sirius A is \(1.7\times\) the Sun’s radius — hot and slightly larger.

“The temperature ratio does the heavy lifting here. Sirius is almost twice as hot, so most of its extra luminosity comes from higher temperature, not bigger size.”

Worked Example: Betelgeuse

Problem: Betelgeuse has \(T \approx 3500\,\mathrm{K}\) and \(L \approx 10^5\,L_\odot\). How big is it?

\[\frac{L}{L_\odot} = 10^5 = \left(\frac{R}{R_\odot}\right)^2 \left(\frac{3500\,\mathrm{K}}{5800\,\mathrm{K}}\right)^4\]

\[10^5 = \left(\frac{R}{R_\odot}\right)^2 \times (0.60)^4 = \left(\frac{R}{R_\odot}\right)^2 \times 0.13\]

\[\left(\frac{R}{R_\odot}\right)^2 = \frac{10^5}{0.13} \approx 7.7 \times 10^5\]

\[\frac{R}{R_\odot} = (7.7 \times 10^5)^{1/2} \approx \mathbf{880}\]

Credit: ESO

Betelgeuse is ~880 times the Sun’s radius (~4 AU). It would swallow Mars and the entire asteroid belt!

“Betelgeuse is cool but ENORMOUS. Its \(T^4\) factor is only \(0.13\times\) the Sun’s, so to reach \(10^5\,L_\odot\) it needs a colossal surface area.”

Quick Check: The Ratio Method

A star is \(3\times\) hotter than the Sun and has the same radius. Using the ratio method, how luminous is it compared to the Sun?

• \(3\times\) more luminous
• \(9\times\) more luminous
• \(81\times\) more luminous
• \(27\times\) more luminous

1 min. Poll.

Solution: \(L/L_\odot = (R/R_\odot)^2 (T/T_\odot)^4 = (1)^2 \times (3)^4 = 81\).

Observable → Model → Inference

The astronomer’s tape measure:

Observable: Betelgeuse appears red (peak in near-IR) and is \(100{,}000\times\) more luminous than the Sun.

Model: \(L/L_\odot = (R/R_\odot)^2 (T/T_\odot)^4\) — the ratio method.

Inference: Betelgeuse must be ~880× the Sun’s radius. A cool but enormous star.

No ruler. No spacecraft. Just light and one equation — with all constants canceled.

Second O→M→I callback. “We went from color and brightness to physical size — using ratios.”

Part 5: Where Does the Curve Come From?

We’ve used the blackbody curve all lecture — but in 1900, it was physics’ most embarrassing failure.

~8 min. Historical perspective. Students should absorb the story, not memorize the equations.

The Ultraviolet Catastrophe

The problem (circa 1900):

Classical physics predicted that a hot object should emit infinite energy at short wavelengths!

Classical prediction (Rayleigh-Jeans):

\[B(\lambda) \propto \frac{T}{\lambda^4}\]

As \(\lambda \to 0\), energy \(\to \infty\). Obviously wrong!

This was called the “ultraviolet catastrophe” — classical physics broke down.

“This was a crisis. The best physics of the time predicted nonsense — infinite energy from a warm object.”

Planck’s Quantum Solution (1900)

Max Planck’s radical idea:

Energy isn’t continuous — it comes in discrete packets: quanta.

\[E = nh\nu\]

where \(n = 0, 1, 2, 3, ...\) (integers only!)

Why this fixes the catastrophe:

At short wavelengths, \(h\nu\) is large.

Creating even ONE quantum requires lots of energy.

At finite temperature, high-energy quanta are exponentially suppressed.

“Planck didn’t fully believe his own solution at first. He called it an ‘act of desperation.’ But it worked.”

The Model Behind the Curve

You don’t need to memorize this equation. But it’s worth seeing — this single formula produces every blackbody curve you’ve explored in the demo.

\[B_\lambda(T) = \frac{2hc^2}{\lambda^5} \times \frac{1}{e^{hc/\lambda k_B T} - 1}\]

This is the Planck function — temperature is the ONLY variable.

• At long wavelengths: matches classical predictions
• At short wavelengths: exponentially suppressed (no catastrophe!)
• Wien’s Law and Stefan-Boltzmann both emerge from this one equation

When you move the temperature slider in the demo, you’re watching the Planck function respond.

“Every curve you saw in the interactive demo is generated by this equation. Wien’s Law, Stefan-Boltzmann — they’re all consequences. One model, all of blackbody physics.”

Birth of Quantum Mechanics

Planck’s solution (1900) required \(E = h\nu\).

Einstein (1905) showed light itself comes in quanta: photons.

Bohr (1913) showed atoms have quantized energy levels.

Heisenberg & Schrödinger (1925–26) developed full quantum mechanics.

The blackbody problem launched the quantum revolution!

Trying to understand why hot things glow the way they do led to the theory that governs atoms, chemistry, and modern technology.

“All of quantum mechanics — semiconductors, lasers, MRI machines — traces back to Planck trying to fix the blackbody spectrum.”

🖥️ Explore: Spectrum of Altair

~2 min. Capstone interactive. ViewSpace (NASA/STScI). Walk through the slider steps:

1. NAKED-EYE VIEW — Altair in the Summer Triangle
2. TELESCOPE VIEW — zooming in on the star
3. SPECTROGRAPH — spreading starlight into a rainbow
4. SPECTRUM — the continuous rainbow with dark absorption lines
5. GRAPH — intensity vs wavelength (a real blackbody-like curve!)
6. INTERPRETATION — what the spectrum tells us

Key connection: The smooth curve is the blackbody continuum we just learned about. The dark lines on top are spectral absorption lines — that’s Lecture 9.

“This is everything we learned today — Wien’s Law, Stefan-Boltzmann, the ratio method — all feeding into reading a spectrum like this. The Observable → Model → Inference pipeline in action.”

Key Takeaways

1. Everything above absolute zero emits thermal radiation. Hotter \(\to\) more and at shorter wavelengths.

2. Blackbody spectrum depends only on temperature.

3. Wien’s Law: \(\lambda_{\text{peak}}\,(\mathrm{nm}) = 2.9 \times 10^6\,\mathrm{nm\cdot K}\, / \, T\,(\mathrm{K})\). Hot \(\to\) blue. Cool \(\to\) red.

4. The Sun peaks at green but appears white because it emits broadly.

5. Stefan-Boltzmann: Power per area \(\propto T^4\). Doubling \(T\) \(\to\) \(16\times\) more luminous.

6. L-T-R: \(L = 4\pi R^2 \sigma T^4\). Use the ratio method to skip the constants.

7. The Planck function is the model behind every blackbody curve — it launched quantum mechanics.

Rapid recap before spectral lines preview.

Coming Up: Spectral Lines

Next lecture: Spectral lines — the chemical fingerprints.

Blackbodies tell us temperature.

Spectral lines tell us composition and motion.

Reading: Lecture 9 Reading Companion

Demos: Blackbody Radiation | EM Spectrum

Preview spectral lines.

Spectral Lines Preview: Absorption vs Emission

Credit: Illustration: NASA, ESA, CSA

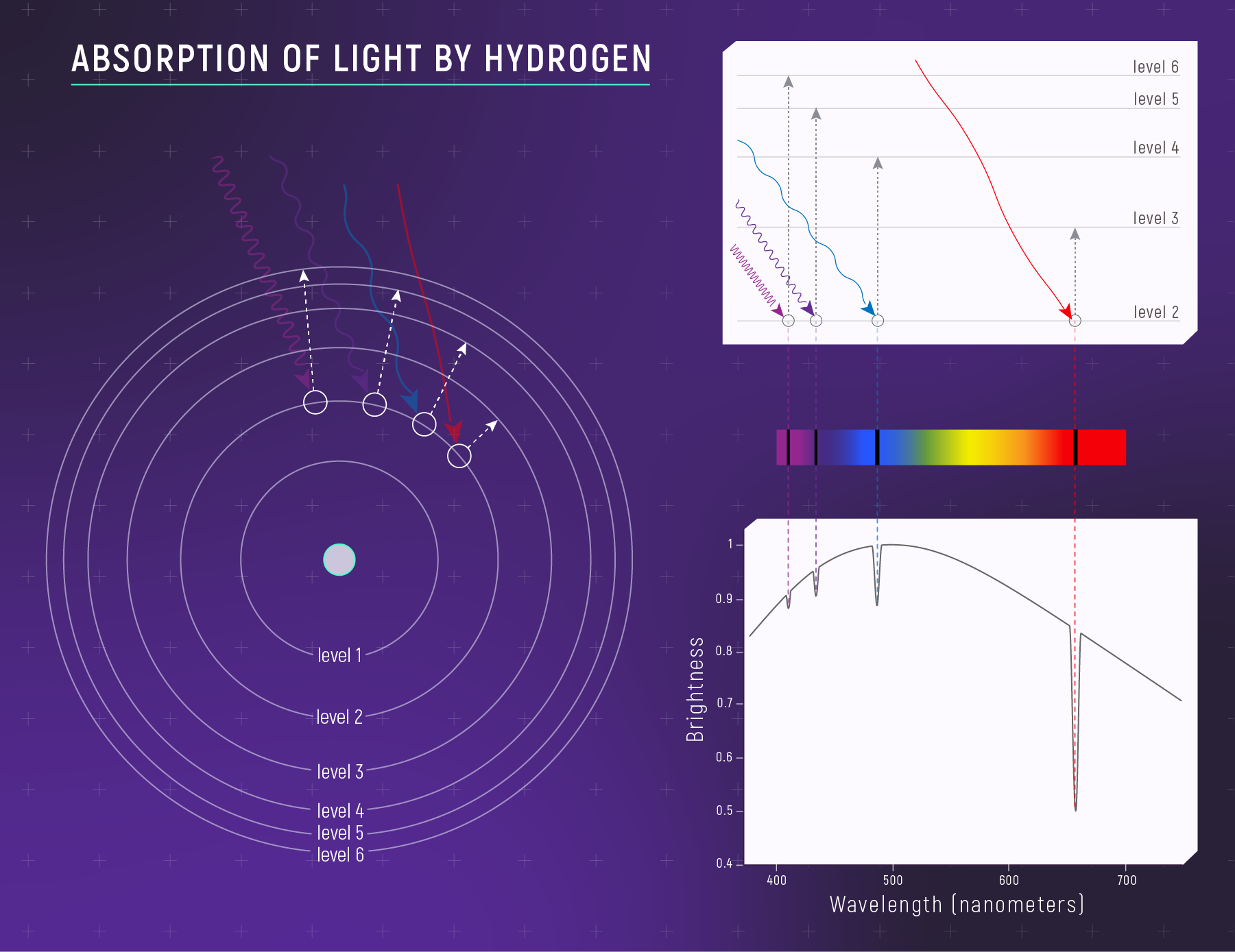
Absorption spectrum

Credit: Illustration: NASA, ESA, CSA

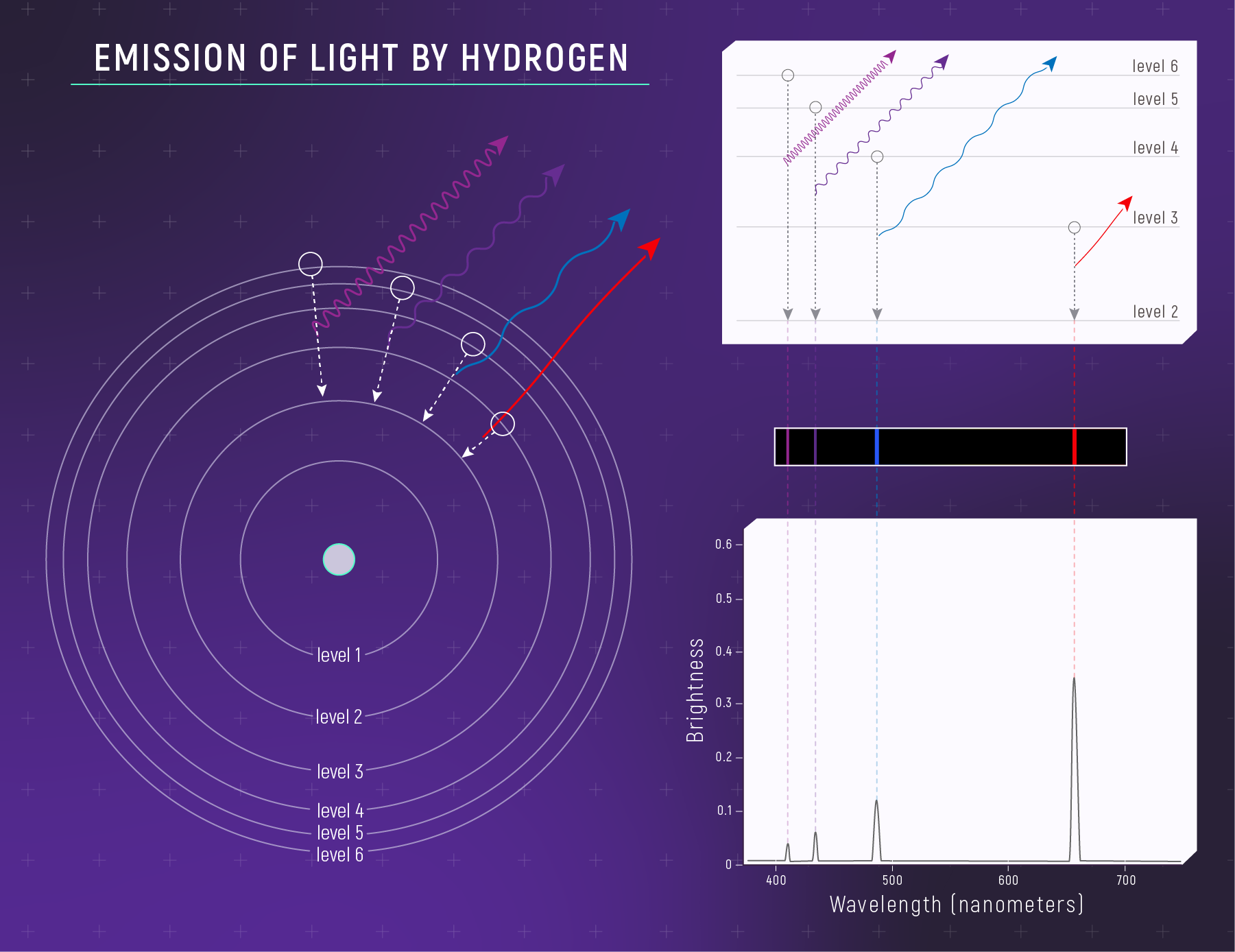
Emission spectrum

Same element, same line wavelengths, different physical setup.

Bridge from blackbody continuum to Lecture 9 line physics.

Questions?

Temperature is written in light.

Wien’s Law + Stefan-Boltzmann + the ratio method = the astronomer’s thermometer.

Remaining time for questions.