Decoding Starlight

Spectral Lines and Chemical Fingerprints

Dr. Anna Rosen

February 18, 2026

Join iClicker

Credit: iClicker

join.iclicker.com/ASES

If you can’t scan: open the link and enter the course code ASES.

30–60 sec. Get everyone connected before starting.

The Missing Colors

In 1814, Joseph von Fraunhofer found dark lines crossing the Sun’s spectrum.

Specific wavelengths where light was missing.

0–1 min. “These dark lines would reveal the composition of stars.”

Credit: Illustration: A. Rosen

0–1 min. Let this image sit. “Look at how many dark lines cross the solar rainbow. Each one is a wavelength that’s been absorbed — stolen from the sunlight — by atoms in the Sun’s atmosphere. Fraunhofer catalogued hundreds of these. Today we’ll learn why they exist and what they tell us.”

Chemical Fingerprints

Each chemical element absorbs and emits at unique wavelengths.

The pattern is like a barcode — match it, identify the element.

This is how we know what stars are made of, from 150 million km away.

1–2 min. “Spectral lines are chemical fingerprints.”

Today’s Learning Objectives

By the end of today, you’ll be able to:

• Describe how emission and absorption spectra form (Kirchhoff’s Laws)
• Explain why spectra have discrete lines (quantized energy levels)
• Apply the hydrogen energy level formula to predict line wavelengths
• Identify the OBAFGKM spectral sequence and its temperature basis
• Explain why hydrogen lines are strongest in A-type stars

2–3 min. “Today: where spectral lines come from and what they tell us.”

Part 1: Three Types of Spectra

Kirchhoff’s Laws

Predict First!

You observe light from a hot, dense source that passes through a cooler, thin gas on its way to you. What kind of spectrum do you expect?

1. Continuous (smooth rainbow)

2. Emission lines (bright lines on dark)

3. Absorption lines (dark lines on bright)

30 s. Commit first, then reveal in Kirchhoff’s Laws: cool gas in front of a hot source produces an absorption spectrum.

Kirchhoff’s Three Laws

1. Continuous Spectrum

Hot, dense object → light at all wavelengths (smooth rainbow)

2. Emission Spectrum

Hot, thin gas → light at specific wavelengths only (bright lines on dark)

3. Absorption Spectrum

Cool gas in front of hot source → dark lines on bright rainbow

3–5 min. “The physical setup determines the spectrum type.”

Credit: Illustration: NASA, ESA, CSA

5–6 min. Visual summary of the three spectrum types.

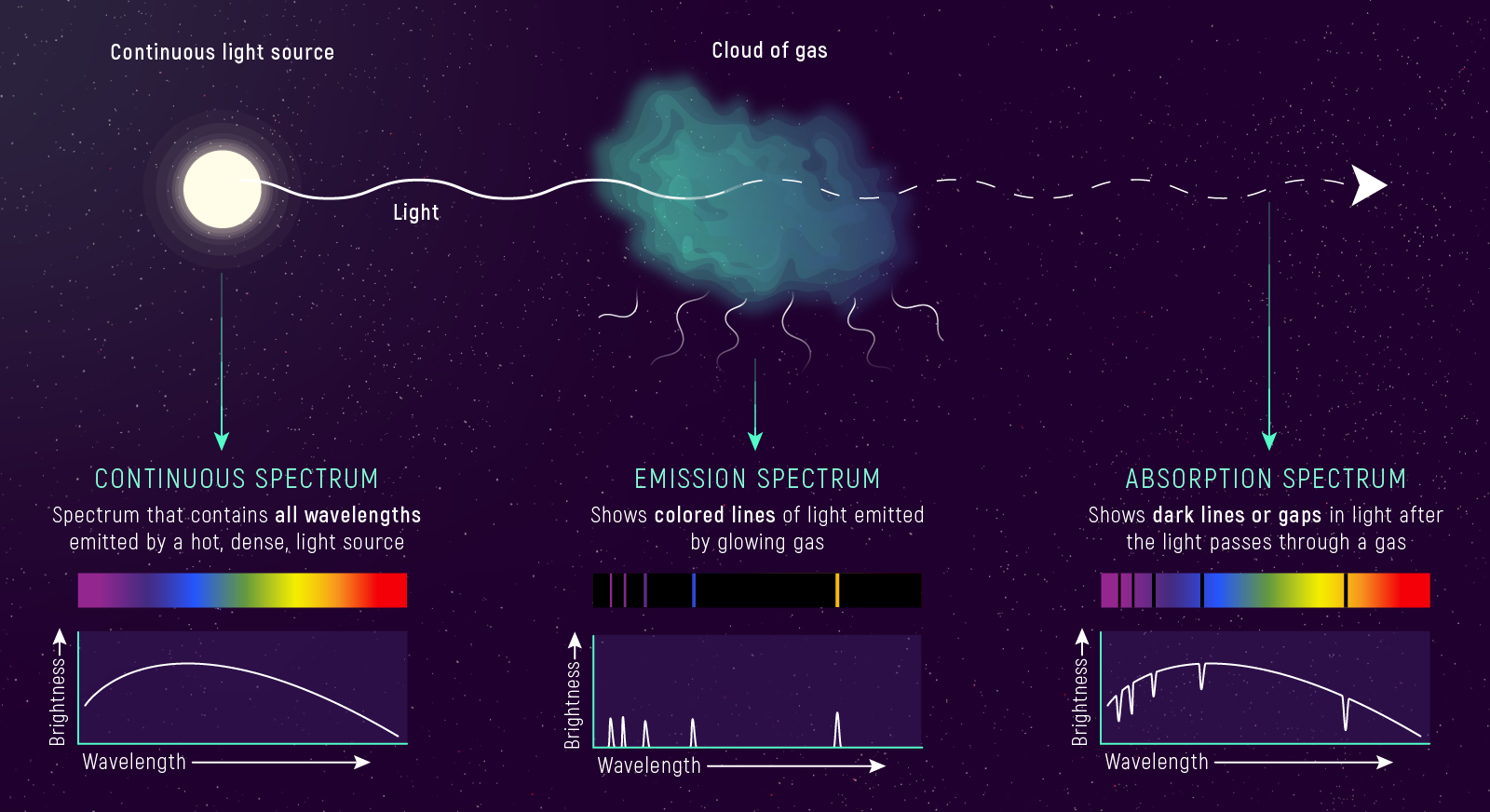
Why Stars Have Absorption Lines

1. Hot interior (dense) → continuous blackbody spectrum (the Planck curve from last lecture!)
2. Cooler outer atmosphere (thin gas) → absorbs specific wavelengths
3. What we see: that smooth blackbody rainbow, but with dark lines carved into it

The pattern of dark lines tells us which elements are in the star’s atmosphere.

6–7 min. “Remember the blackbody curve from Lectures 7–8? That’s the continuous spectrum — the starting point. Today we’re learning what carves those dark lines into it. Every star works like a light bulb behind a filter.”

Quick Check: Kirchhoff’s Laws

The dark lines in the Sun’s spectrum are caused by:

• The Sun’s core being too cool to emit those wavelengths
• Cool gas in the Sun’s outer atmosphere absorbing specific wavelengths
• Earth’s atmosphere blocking the light
• The Sun rotating and shifting the wavelengths

1 min. iClicker poll.

🖥️ Live Demo: Spectral Lines Lab

~3 min. Live demo. Walk through the three Kirchhoff setups:

1. Start with the continuous source — smooth rainbow, no lines
2. Switch to hot thin gas — bright emission lines appear on a dark background
3. Place cool gas in front of hot source — dark absorption lines on the rainbow

Then switch to element fingerprints:

4. Show hydrogen lines — ask: “How many lines does hydrogen have in the visible?”
5. Overlay a second element — ask: “Could you tell these apart by pattern alone?”

Key message: The pattern is the fingerprint, not any single line.

What Did You Notice?

Think-Pair-Share (~90 seconds)

Turn to your neighbor and discuss:

“Could you identify an element from just one spectral line? Why or why not?”

No — different elements can share individual wavelengths. The full pattern of lines is the fingerprint, like a barcode. You need multiple lines to make a unique match.

~2 min. Think-Pair-Share. Let pairs discuss for 60–90 sec, then cold-call 1–2 pairs. This question targets the common misconception that one line = one element. Reinforce: it’s pattern matching, not single-line identification. The barcode analogy lands hard here. This bridges into the next section on chemical fingerprints.

Each Element Has a Unique Pattern

Element	Signature Lines
Hydrogen	656 nm (red), 486 nm (blue-green), 434 nm (violet)…
Sodium	Bright yellow doublet at 589 nm
Calcium	Violet H and K lines (397, 393 nm)
Iron	Hundreds of lines throughout visible

Match the pattern → identify the element.

7–8 min. “Like barcodes for atoms.”

Quick Check: Element Identification

How do astronomers determine which elements are present in a star?

• By measuring the star’s temperature
• By matching the pattern of spectral lines to laboratory measurements
• By observing the star’s color
• By measuring how bright the star is

1 min. iClicker poll.

Part 2: Why Discrete Lines?

The deepest puzzle in spectroscopy

The Puzzle

Why do atoms absorb and emit at specific wavelengths only?

Why not a continuous range?

Classical physics couldn’t explain this.

The answer required a revolution: quantum mechanics.

8–9 min. “This puzzle led to quantum mechanics.”

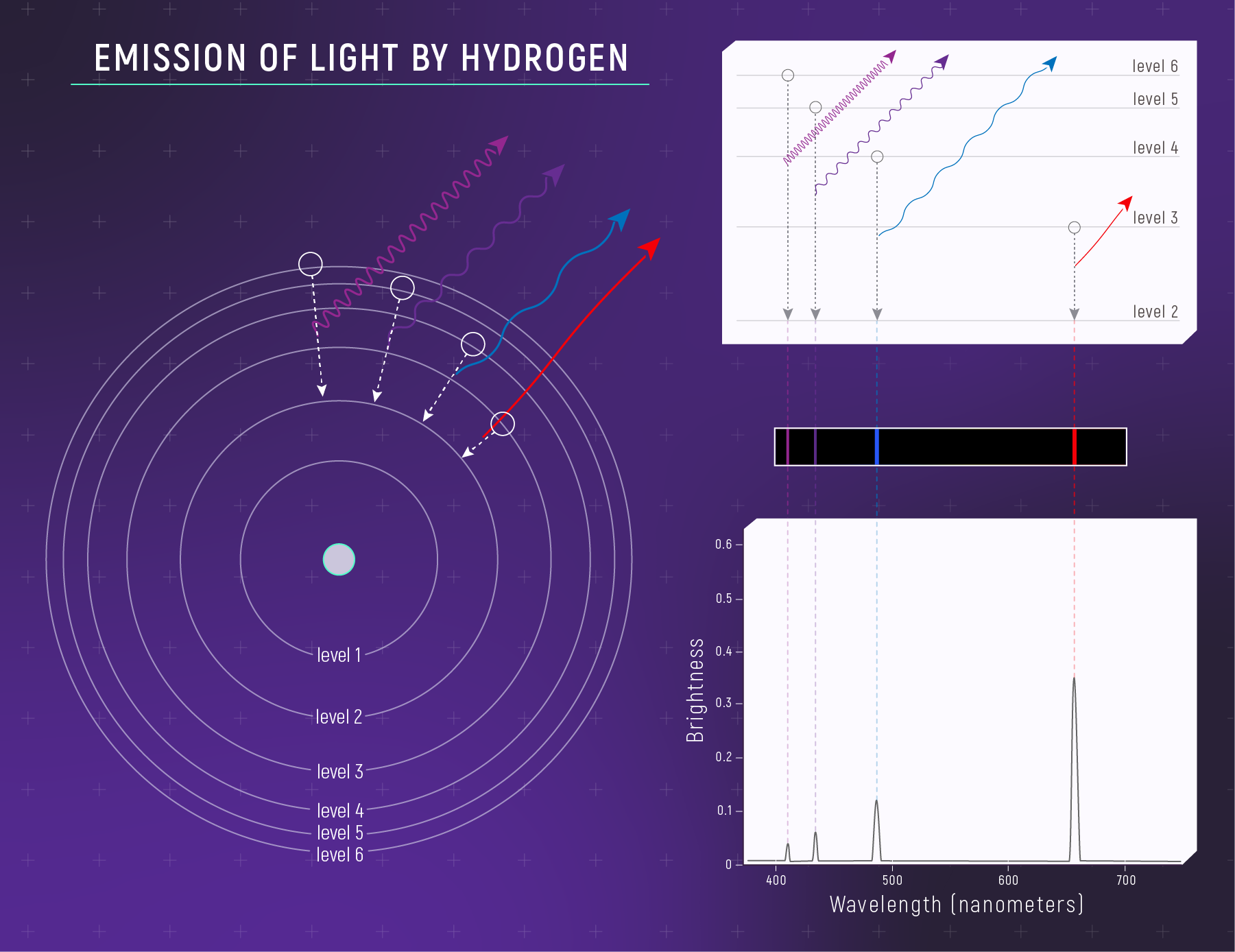
Energy Is Quantized

Electrons can only occupy specific energy levels — like rungs on a ladder, not a ramp.

To move between levels, an electron must absorb or emit a photon with exactly the right energy.

Specific energies → specific wavelengths → discrete lines.

9–10 min. “Quantized energy levels are the key insight.”

The Ladder Analogy

Credit: Illustration: NASA, ESA, CSA

You can stand on the rungs, never between them.

Electrons in atoms are the same — discrete levels only.

10–11 min. “The ladder analogy for energy levels.”

Photon Energy and Wavelength

\[E_{photon} = \frac{hc}{\lambda}\]

\(h\) is Planck’s constant, \(c\) is the speed of light, and \(\lambda\) is wavelength. Shorter \(\lambda\) means higher photon energy.

Higher energy ↔︎ shorter wavelength

Lower energy ↔︎ longer wavelength

The photon energy must exactly match the gap between two levels.

11–12 min. “The energy-wavelength connection.”

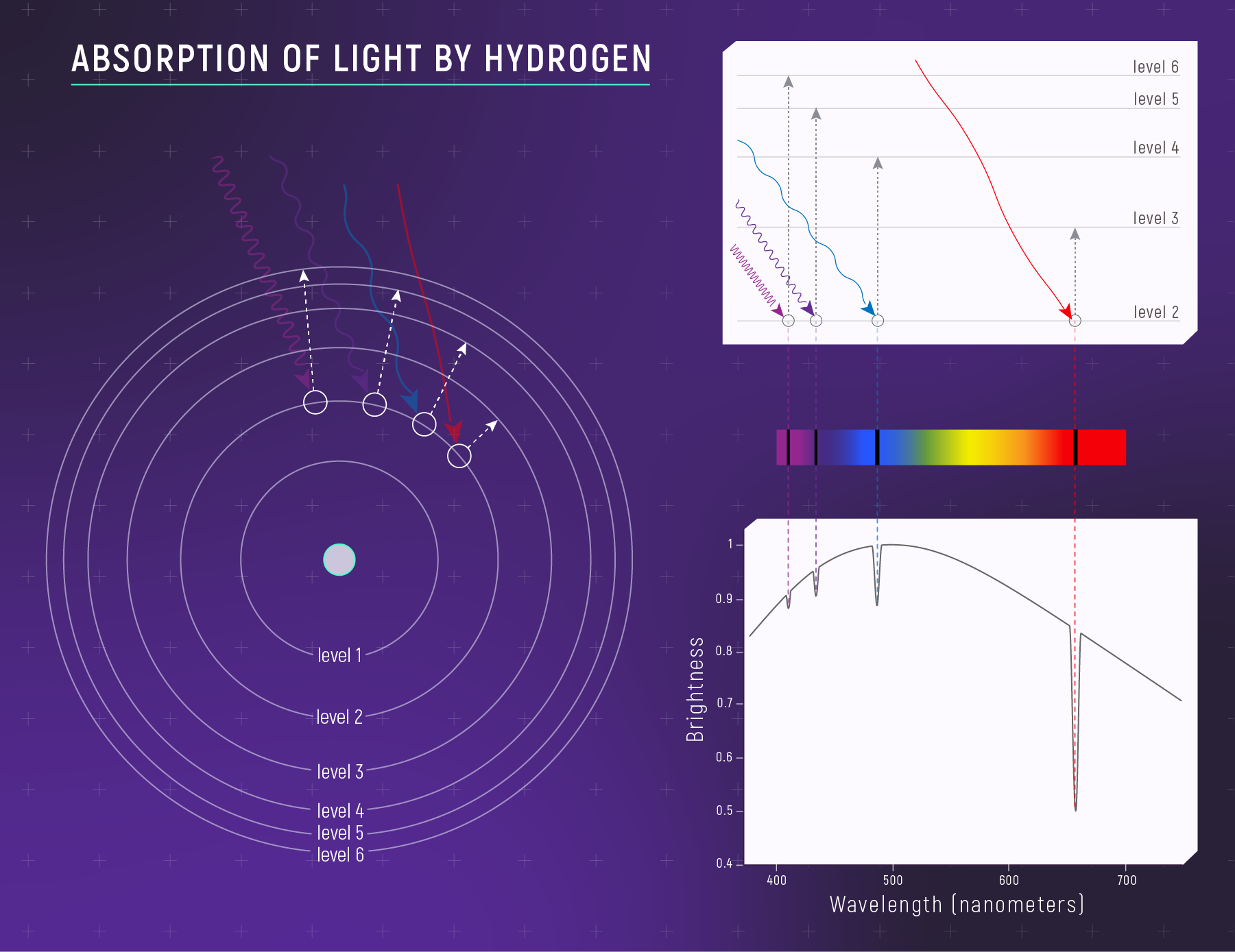
Hydrogen Energy Levels

\[E_n = -\frac{13.6 \text{ eV}}{n^2}\]

where \(n = 1, 2, 3, ...\)

Level	Energy
\(n=1\) (ground)	-13.6 eV
\(n=2\)	-3.4 eV
\(n=3\)	-1.51 eV
\(n=4\)	-0.85 eV
\(n=\infty\) (ionized)	0 eV

12–13 min. “Hydrogen’s energy levels follow a simple formula.”

Credit: Illustration: NASA, ESA, CSA

Levels get closer together as \(n\) increases.

13–14 min. Energy level diagram for hydrogen.

The Balmer Series (Visible Lines)

Transitions ending at n = 2 produce visible light:

Transition	Wavelength	Color	Name
3 → 2	656 nm	Red	Hα
4 → 2	486 nm	Blue-green	Hβ
5 → 2	434 nm	Violet	Hγ
6 → 2	410 nm	Violet	Hδ

Hα is the famous red hydrogen line — why nebulae glow pinkish-red.

14–15 min. “The Balmer series is what we see in visible light.”

Worked Example: Calculating Hα

Problem: Calculate the wavelength when a hydrogen electron drops from n=3 to n=2.

\[E_3 = -\frac{13.6}{9} = -1.51 \text{ eV}\] \[E_2 = -\frac{13.6}{4} = -3.4 \text{ eV}\]

\[E_{photon} = E_3 - E_2 = -1.51 - (-3.4) = 1.89 \text{ eV}\]

\[\lambda = \frac{1240}{1.89} = 656 \text{ nm}\]

15–16 min. Walk through the calculation.

Quick Check: Hydrogen Transitions

Which transition produces the shortest wavelength (highest energy) photon?

• n = 2 → n = 1
• n = 3 → n = 2
• n = 4 → n = 3
• n = 5 → n = 4

Largest energy gap → highest energy photon → shortest wavelength.

1–2 min. iClicker poll, then explain.

Quick Check: Why Discrete Lines?

Spectral lines are discrete (specific wavelengths only) because:

• Telescopes can only detect certain wavelengths
• Atoms can only absorb red, green, and blue light
• Electrons in atoms can only occupy specific quantized energy levels
• Light travels at a constant speed

1 min. iClicker poll.

Part 3: Stellar Classification

OBAFGKM

The OBAFGKM Sequence

O - B - A - F - G - K - M

Stars classified by surface temperature:

O = hottest (blue) → M = coolest (red)

Mnemonic: “Oh Be A Fine Girl/Guy, Kiss Me”

16–17 min. “The spectral classification sequence.”

Spectral Types

Type	Color	Temperature	Features
O	Blue	30,000–50,000+ K	Ionized helium
B	Blue-white	10,000–30,000 K	Neutral helium
A	White	7,500–10,000 K	Strongest H lines
F	Yellow-white	6,000–7,500 K	H + metals
G	Yellow	5,000–6,000 K	Ca, Fe (Sun!)
K	Orange	3,500–5,000 K	Strong metals
M	Red	2,500–3,500 K	Molecular bands

17–18 min. “Each type has distinctive spectral features.”

Credit: Wikimedia Commons (public domain)

17–18 min. “This chart shows the Morgan–Keenan system — spectral type plus luminosity class. Notice the dramatic size and color differences.”

Real Stellar Spectra

Credit: NOAO/AURA/NSF

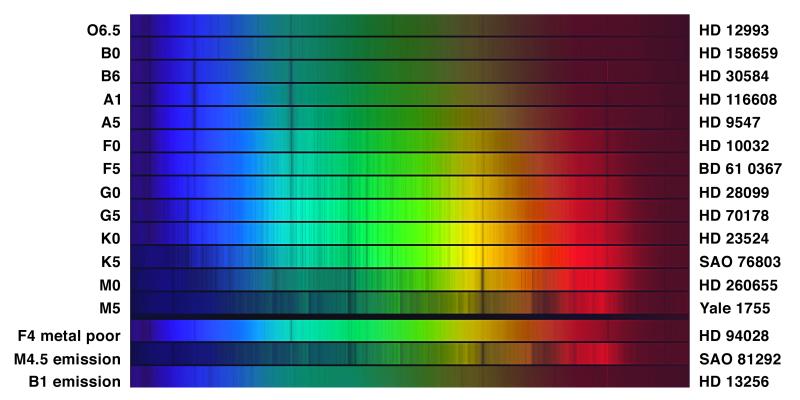
Challenge: Which spectrum shows the strongest hydrogen (Balmer) lines? Why that one and not the hottest?

18 min. Show the image first. Give students 15–20 seconds to look. Then reveal the challenge question. Cold-call: “Which row has the strongest hydrogen lines?” (A stars.) “But O stars are hotter — why don’t they win?” This primes the ionization physics slide that follows. “Hot O stars show few, broad lines — most hydrogen is ionized. A stars show the strongest Balmer lines. Cool M stars show molecular absorption bands instead of sharp atomic lines.”

Quick Check: Spectral Types

A star’s spectrum shows strong calcium and iron lines but no helium lines. Which spectral type is most consistent?

• O or B
• A
• G or K
• This can’t be determined from spectral lines

Helium requires very high temperatures to excite — no He lines rules out O and B. Strong metal lines point to cooler stars (G or K).

1–2 min. iClicker poll. This question forces students to use the spectral types table rather than just recall the sequence. Common wrong answer: “A” (students remember A has strongest H lines but don’t distinguish H from metals). Debrief: “This is exactly how real classification works — you read the line pattern, not just the color.”

Why Do H Lines Peak at A Stars?

Hydrogen is the most abundant element everywhere.

Yet H lines are strongest in A stars (~10,000 K), not the hottest.

Why?

18–19 min. “This puzzled early astronomers.”

The Ionization Physics

Too Hot (O, B)

H is ionized — no bound electron to absorb.

Too Cool (K, M)

H electrons in ground state — can’t absorb Balmer (need n=2).

Just Right (A)

H neutral + electrons excited to n=2 → maximum Balmer absorption!

19–20 min. “Temperature affects which lines appear, not just abundance.”

Quick Check: Why Weak H in O Stars?

Hydrogen absorption lines are weak in O-type stars because:

• O stars contain very little hydrogen
• O stars are so hot that hydrogen is mostly ionized
• O stars are too cool to excite hydrogen
• O stars have thick atmospheres that block H lines

1 min. iClicker poll.

Observable → Model → Inference

The astronomer’s chemical lab:

Observable: A star’s spectrum shows dark lines at 656 nm, 486 nm, 434 nm, plus lines at 393/397 nm.

Model: Each element absorbs at unique wavelengths (quantum mechanics). OBAFGKM classifies stars by which lines dominate.

Inference: Hydrogen and calcium are present. The line strengths indicate ~10,000 K → A-type star.

No sample. No visit. Just photons and pattern matching — from any distance.

~1 min. Reinforce the O→M→I framework. This is the course throughline: L5-L6 (motion reveals mass), L7-L8 (light reveals temperature), L9 (spectral lines reveal composition).

Key Takeaways

1. Kirchhoff’s Laws: Hot dense → continuous; hot thin → emission; cool gas in front → absorption.

2. Each element has unique spectral lines — match the pattern, identify the element.

3. Energy is quantized: Electrons occupy discrete levels → discrete lines.

4. Hydrogen: \(E_n = -13.6/n^2\) eV. Balmer series (to n=2) gives visible lines.

5. OBAFGKM: Hot (O, blue) to cool (M, red). H lines peak at A stars due to ionization physics.

20–22 min. Rapid recap.

Coming Up: The Doppler Effect

Next lecture: What happens when spectral lines shift?

Motion causes Doppler shifts → reveals velocities

• Stellar wobbles → exoplanets
• Galaxy rotation → dark matter

Reading: Lecture 10 Reading Companion

Demos: Spectral Lines Lab | Blackbody Radiation

22–23 min. Preview Doppler and telescopes.

Numerical Verification

Calculating hydrogen spectral lines from first principles

~25 min mark. Guided Practice block (~10 min, slides through Ionization Energies). Walk through the Hα calculation live — students follow along. The full Balmer table is a “reveal and confirm” slide, not a derivation. Lyman and ionization slides are quick conceptual extensions. If short on time, skip to Key Takeaways after the Balmer table.

Hydrogen Energy Levels: Full Calculation

The energy level formula: \(\quad E_n = -\dfrac{13.6 \text{ eV}}{n^2}\)

Calculate the first five levels:

n	Calculation	Energy (eV)
1	\(-13.6/1^2\)	-13.60 eV
2	\(-13.6/2^2\)	-3.40 eV
3	\(-13.6/3^2\)	-1.51 eV
4	\(-13.6/4^2\)	-0.85 eV
5	\(-13.6/5^2\)	-0.54 eV

~26 min. “Negative energies mean the electron is bound. Zero would mean ionized (free electron).” This table is review from the main lecture — confirm, don’t re-derive.

Why Negative Energies?

Convention: A free electron at rest has \(E = 0\).

• Negative energy = bound to the atom (need to ADD energy to escape)
• \(E = 0\) = barely escaped, no kinetic energy
• Positive energy = escaped with kinetic energy to spare

Ionization energy = energy needed to go from \(E_n\) to \(E = 0\)

From ground state: \(E_{\text{ionize}} = 0 - (-13.6) = 13.6\) eV

~27 min. “It takes 13.6 eV to rip an electron out of hydrogen’s ground state.” Quick conceptual aside — don’t dwell.

Hα Calculation: Complete

Transition: \(n = 3 \to n = 2\) (electron falls from level 3 to level 2)

Step 1: Calculate energy difference

\[\Delta E = E_3 - E_2 = (-1.51 \text{ eV}) - (-3.40 \text{ eV}) = +1.89 \text{ eV}\]

Positive because the electron releases energy (emits a photon)

~28 min. “The electron loses 1.89 eV of potential energy, which goes into the photon.” This is the key calculation — work it step-by-step on the board or walk through fragments slowly.

Hα Calculation: Wavelength

Step 2: Convert energy to wavelength — Using \(E = hc/\lambda\), so \(\lambda = hc/E\)

The convenient form: \(\quad \lambda = \dfrac{1240 \text{ eV·nm}}{E \text{ (eV)}}\)

\[\lambda = \frac{1240 \text{ eV·nm}}{1.89 \text{ eV}} = 656.1 \text{ nm}\]

Unit check: \(\frac{\text{eV·nm}}{\text{eV}} = \text{nm}\) ✓

Hα = 656 nm — the famous red hydrogen line! (Lab reference: 656.28 nm)

~29 min. “This is the red glow you see in images of nebulae. We calculated it from quantum mechanics!” Emphasize the unit check — modeling good practice.

Calculating the Entire Balmer Series

Transitions to \(n = 2\) — our predictions:

Transition	\(\Delta E\) (eV)	Calculation	Predicted λ	Measured λ
3→2 (Hα)	\(-1.51-(-3.40) = 1.89\)	\(1240/1.89\)	656 nm
4→2 (Hβ)	\(-0.85-(-3.40) = 2.55\)	\(1240/2.55\)	486 nm
5→2 (Hγ)	\(-0.54-(-3.40) = 2.86\)	\(1240/2.86\)	434 nm
6→2 (Hδ)	\(-0.38-(-3.40) = 3.02\)	\(1240/3.02\)	411 nm

Transition	\(\Delta E\) (eV)	Calculation	Predicted λ	Measured λ
3→2 (Hα)	\(-1.51-(-3.40) = 1.89\)	\(1240/1.89\)	656 nm	656.3 nm
4→2 (Hβ)	\(-0.85-(-3.40) = 2.55\)	\(1240/2.55\)	486 nm	486.1 nm
5→2 (Hγ)	\(-0.54-(-3.40) = 2.86\)	\(1240/2.86\)	434 nm	434.0 nm
6→2 (Hδ)	\(-0.38-(-3.40) = 3.02\)	\(1240/3.02\)	411 nm	410.2 nm

We just predicted the exact colors of starlight from an equation on a blackboard.

Every value matches the lab measurement within 1%.

~30 min. This is the money slide. Show the predicted column first (no measured values). Pause. Ask: “Do you think these will match reality?” Then reveal the measured column alongside. Let the match register. The closing callout is the emotional payoff — don’t rush past it.

The Lyman Series: UV Lines

Transitions to \(n = 1\) (ground state):

Lyman-α (2→1):

\[\Delta E = E_2 - E_1 = (-3.40) - (-13.60) = 10.2 \text{ eV}\]

\[\lambda = \frac{1240 \text{ eV·nm}}{10.2 \text{ eV}} = 121.6 \text{ nm}\]

This is far-ultraviolet! (Absorbed by Earth’s atmosphere)

Astronomers need space telescopes to see Lyman-α from cosmic sources.

~31 min. “The Lyman series is in the UV because transitions to n=1 involve much more energy.” Quick — the point is UV vs visible, not the calculation.

Series Limit and Ionization

What happens as n → ∞? For the Balmer series (transitions to \(n = 2\)):

\[\Delta E_{\text{max}} = E_\infty - E_2 = 0 - (-3.40) = 3.40 \text{ eV}\]

\[\lambda_{\text{min}} = \frac{1240}{3.40} = 365 \text{ nm}\]

365 nm is the “series limit” — the shortest Balmer wavelength.

Photons shorter than this ionize the atom from \(n = 2\)!

~32 min. “Beyond the series limit, the electron is freed entirely.” Connects to ionization physics from the OBAFGKM section.

Ionization Energies by Level

Starting Level	Energy (eV)	Ionization Energy	Photon λ to ionize
n = 1 (ground)	-13.60	13.6 eV	< 91 nm (far-UV)
n = 2	-3.40	3.4 eV	< 365 nm (UV)
n = 3	-1.51	1.51 eV	< 821 nm (IR)

Excited atoms are easier to ionize!

An H atom with an electron in \(n = 3\) can be ionized by infrared light.

~33 min. “This is why temperature matters for spectral lines. Hot stars have many excited atoms.” This table ties the numerical section back to the OBAFGKM ionization argument. Good place to end Numerical Verification if time is tight.

Deeper Dive

The Rydberg formula and other elements

~34 min mark. Optional enrichment block (~8–10 min). Use if time permits or as a reference for curious students. Cover Rydberg formula quickly (1–2 min), show the Bohr derivation as “here’s where 13.6 comes from” without derivation details (1 min), then hydrogen-like ions and multi-electron atoms as conceptual bookends (2 min each). Metallicity slide is a fun cultural aside (~1 min). If under 10 min remain, skip to Questions slide.

The Rydberg Formula

A single formula for all hydrogen wavelengths:

\[\frac{1}{\lambda} = R_H \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)\]

Where:

• \(R_H = 1.097 \times 10^7\) m⁻¹ (Rydberg constant)
• \(n_f\) = final level (lower)
• \(n_i\) = initial level (higher)

Different series:

• \(n_f = 1\): Lyman series (UV)
• \(n_f = 2\): Balmer series (visible)
• \(n_f = 3\): Paschen series (IR)

~35 min. “Rydberg found this pattern empirically in 1888. Bohr explained it in 1913.” Show the formula structure — don’t derive. The historical point is powerful: pattern found 25 years before the explanation.

Rydberg Example: Hα

\[\frac{1}{\lambda} = R_H \left( \frac{1}{2^2} - \frac{1}{3^2} \right)\]

\[= 1.097 \times 10^7 \text{ m}^{-1} \left( \frac{1}{4} - \frac{1}{9} \right) = 1.097 \times 10^7 \text{ m}^{-1} \left( \frac{5}{36} \right)\]

\[= 1.524 \times 10^6 \text{ m}^{-1}\]

\[\lambda = \frac{1}{1.524 \times 10^6 \text{ m}^{-1}} = 6.56 \times 10^{-7} \text{ m} = 656 \text{ nm}\]

~36 min. “Same answer we got before! The Rydberg formula is equivalent to our energy level approach.” Quick confirmation — don’t re-derive. The point: two roads to the same destination.

Where Does 13.6 eV Come From?

Bohr model derivation (simplified):

Balance Coulomb force with centripetal acceleration: \(\quad \dfrac{e^2}{4\pi\epsilon_0 r^2} = \dfrac{m_e v^2}{r}\)

Quantize angular momentum: \(\quad m_e v r = n\hbar \quad \text{where } \hbar = h/2\pi\)

Solving these together gives:

\[E_n = -\frac{m_e e^4}{8\epsilon_0^2 h^2} \times \frac{1}{n^2}\]

The constant evaluates to 13.6 eV.

~37 min. “The 13.6 eV comes from fundamental constants: electron mass, charge, Planck’s constant.” Show, don’t derive. The takeaway: one number from three constants — that’s elegant physics.

Other Elements: Scaling

For hydrogen-like ions (one electron, nuclear charge \(Z\)): \(\quad E_n = -\dfrac{13.6 \text{ eV} \times Z^2}{n^2}\)

Ion	Z	Ground state energy	Ionization energy
H	1	-13.6 eV	13.6 eV
He⁺	2	-54.4 eV	54.4 eV
Li²⁺	3	-122.4 eV	122.4 eV

More protons → electron bound more tightly → higher ionization energy.

~38 min. “Helium with one electron stripped (He⁺) has 4× the ionization energy of hydrogen.” The Z² scaling is the key insight — more protons, tighter grip.

Multi-Electron Atoms: Complications

For atoms with multiple electrons:

• Electrons shield each other from the nucleus
• Energy levels don’t follow simple \(1/n^2\) pattern
• Each element has a unique energy level structure
• This is why each element has unique spectral lines!

The uniqueness of spectra is a feature, not a bug.

It’s what allows us to identify elements across the universe.

~39 min. “The complexity of multi-electron atoms is what gives each element its fingerprint.” This closes the loop: hydrogen is simple → real atoms are complex → complexity = uniqueness = spectroscopy works.

Why “Metals” in Astronomy?

Astronomical definition of “metal”: Anything heavier than helium!

Why this weird definition?

• H and He are ~98% of ordinary matter
• Everything else is trace amounts
• Spectroscopist’s view: H lines, He lines, and “all the rest”

Metallicity = fraction of elements heavier than He

• Sun: ~2% metals (by mass)
• Old stars: <0.1% metals
• Young stars: up to ~3% metals

Yes, this means oxygen is a “metal” and carbon is a “metal.” Chemists love this about us.

~40 min. “When astronomers say ‘metal-rich star,’ they might mean iron, calcium, or even carbon!” Fun cultural aside — students enjoy learning jargon. The punchline always gets a laugh. Good energy note to end on before Q&A.

Questions?

Spectral lines are chemical fingerprints.

Quantum mechanics explains why they’re discrete.

Remaining time for questions.