Lecture 4 (Day 1):
Light as Information

Spectrum • Photons • Interactions • Temperature

Dr. Anna Rosen

February 3, 2026

Learning Objectives

By the end of today, you will be able to:

• Relate wavelength (\(\lambda\)), frequency (\(\nu\)), and photon energy (\(E\))
• Explain why the visible band is a tiny slice of the EM spectrum
• Describe the main ways light interacts with matter (absorb, emit, transmit, reflect/refract, scatter)
• Use Wien’s law to estimate temperature from a thermal spectrum’s peak

Read these aloud. Framing: this is “inference tool #1” for the course. Timing: ~2 min.

How can a rainbow tell you a star’s temperature?

Let this sit for 5 seconds. Today’s arc: what we measure (light) → what we infer (temperature) using a model (blackbody).

The Course Throughline

Today’s Piece

Measure → Infer → Balance → Evolve

• Measure: intensity vs wavelength (a spectrum)
• Infer: temperature (soon: composition)

Credit: Course illustration (A. Rosen)

Point to Wavelength. Tie to Lecture 1: “we only measure four things”.

A “Pretty Picture” Is Still Data

Brightness patterns + color patterns = physics patterns.

Ask: What could color mean? (temperature, dust, emission lines) Today: temperature first.

Today’s Game Plan

We’re building inference tool #1:

1. What light is (spectrum)
2. How light carries energy (photons)
3. How matter changes light (interactions)
4. How color encodes temperature (blackbody + Wien)

End: quick demos (if time) to lock the intuition.

Set expectations: lots of short slides on purpose — one idea at a time. Pacing target (flexible): Part 1 (~15 min), Part 2 (~10 min), Part 3 (~15 min), Part 4 (~20 min), demos (~5–10 min).

The Wave Relation

The symbol \(c\) is the speed of light in vacuum.

\[ c = \lambda \nu \tag{1}\]

• In vacuum, \(c \approx 3\times10^{10}\ \mathrm{cm/s}\)
• Solve for wavelength: \(\lambda = c/\nu \;\Rightarrow\; \lambda \propto \nu^{-1}\)
• Solve for frequency: \(\nu = c/\lambda \;\Rightarrow\; \nu \propto \lambda^{-1}\)
• Negative exponents are a compact way to show “inverse” relationships; you can also write \(\lambda \propto 1/\nu\) or \(\nu \propto 1/\lambda\)

Units check quickly: [cm/s] = [cm][1/s]. Micro-prompt: “If wavelength doubles, what happens to frequency?”

Part 1: The Electromagnetic Spectrum

What kind of “messenger” is light?

What Is Light?

Wave Picture

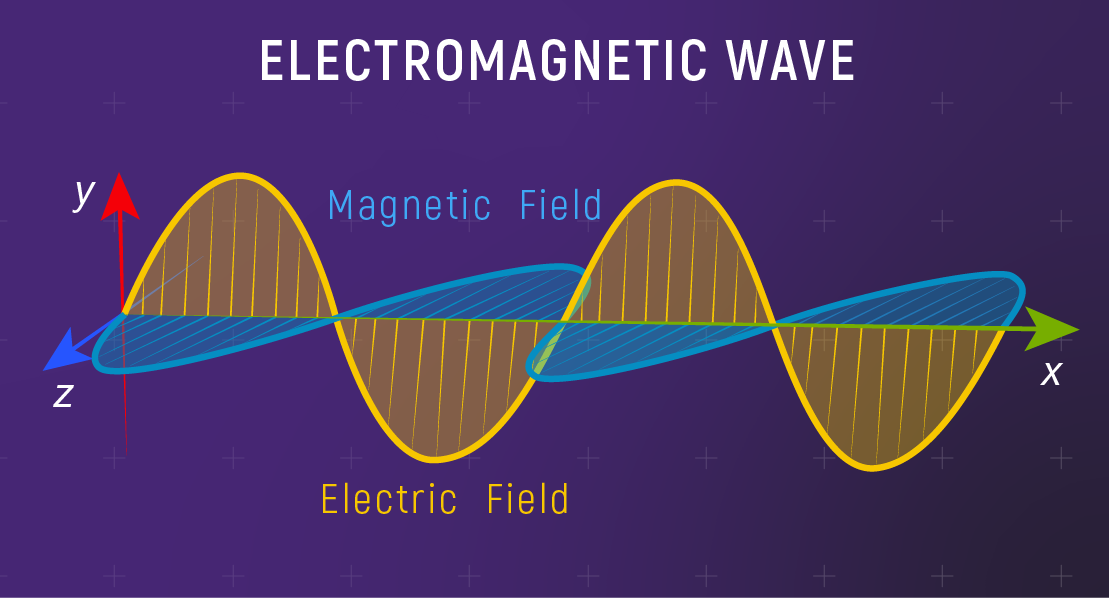
Light is an electromagnetic wave.

Three related quantities:

• wavelength \(\lambda\) (distance between crests)
• frequency \(\nu\) (cycles per second)
• speed \(c\) (in vacuum)

Credit: JWST/STScI

Keep it visual. Point out: E and B are perpendicular; propagation direction is perpendicular to both.

Mechanical Waves vs EM Waves

Credit: JWST/STScI

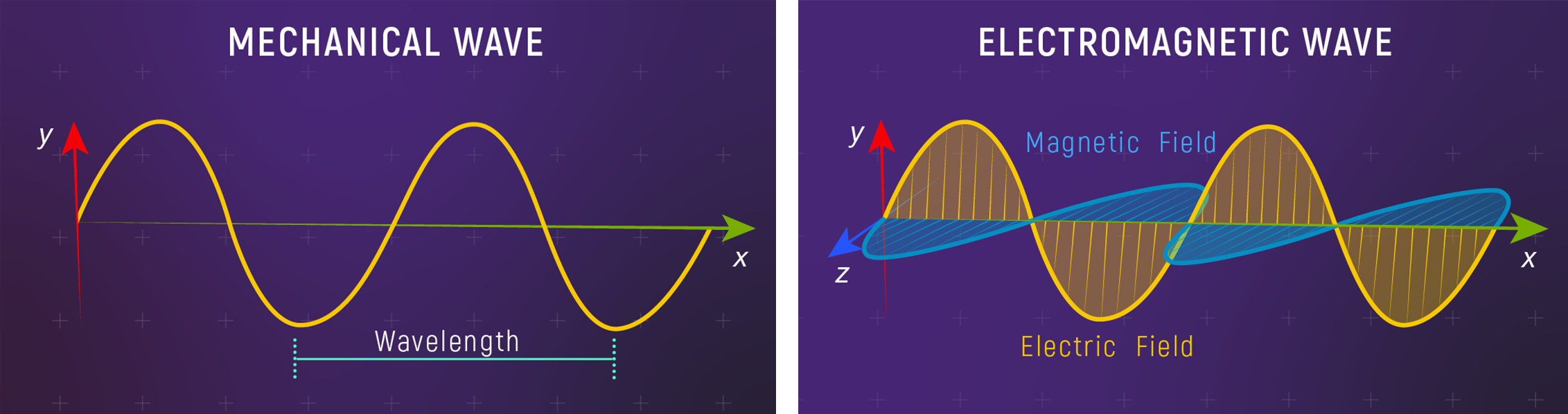
Mechanical waves need a medium.

EM waves don’t — that’s why light crosses the vacuum of space.

The Wave Relation

The symbol \(c\) is the speed of light in vacuum.

\[ c = \lambda \nu \tag{2}\]

• In vacuum, \(c \approx 3\times10^{10}\ \mathrm{cm/s}\)
• Solve for wavelength: \(\lambda = c/\nu \;\Rightarrow\; \lambda \propto \nu^{-1}\)
• Solve for frequency: \(\nu = c/\lambda \;\Rightarrow\; \nu \propto \lambda^{-1}\)
• Negative exponents are a compact way to show “inverse” relationships; you can also write \(\lambda \propto 1/\nu\) or \(\nu \propto 1/\lambda\)

Units check quickly: [cm/s] = [cm][1/s]. Micro-prompt: “If wavelength doubles, what happens to frequency?”

Units Sanity Check

Fast

If \(c = \lambda\nu\), then the units must satisfy:

\[[\mathrm{cm/s}] = [\mathrm{cm}]\,[\mathrm{s^{-1}}]\]

If the units don’t match, the physics can’t be right.

Tie back to Lecture 2: units are a “smoke detector.”

Wavelength Units

So We Speak the Same Language

Visible light is roughly:

• \(400\)–\(700\ \mathrm{nm}\)

Conversion: \(1\ \mathrm{nm}=10^{-7}\ \mathrm{cm}\).

Course convention: CGS (cm, s, erg, K).

Energy unit: \(1\ \mathrm{erg} = 1\ \mathrm{g\cdot cm^2/s^2}\).

Keep this fast. Students often get lost in unit switches; give them one anchor conversion.

🧠 Predict: No Calculator

If the wavelength doubles, the frequency…

• doubles
• halves
• stays the same
• becomes zero

Press C to reveal. Use it to reinforce inverse proportionality. Answer: halves.

The Electromagnetic Spectrum

Credit: JWST/STScI

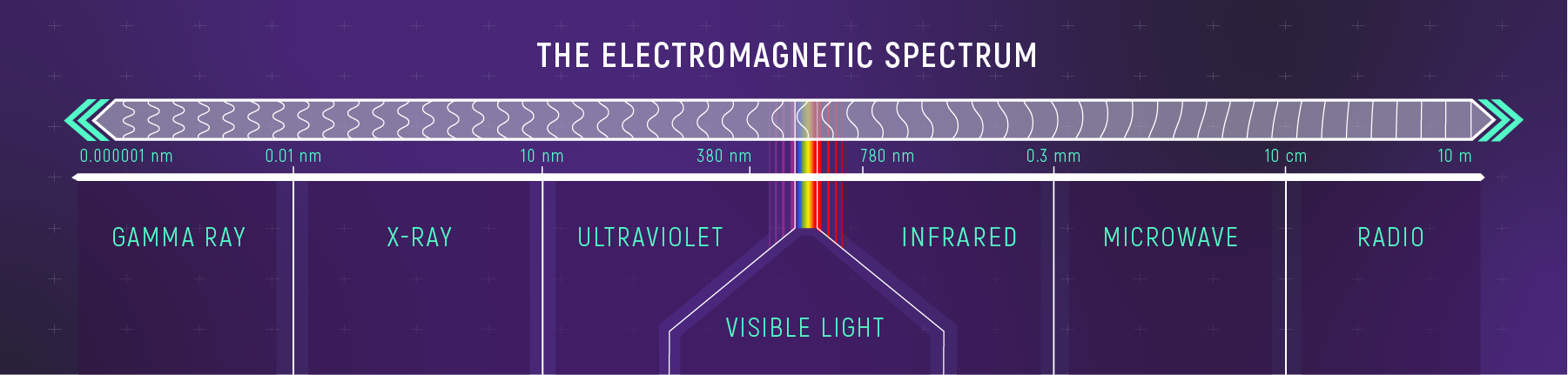
Visible light is a tiny slice.

Point out the visible zoom-in. Ask: “So if we only used visible, what would we miss?”

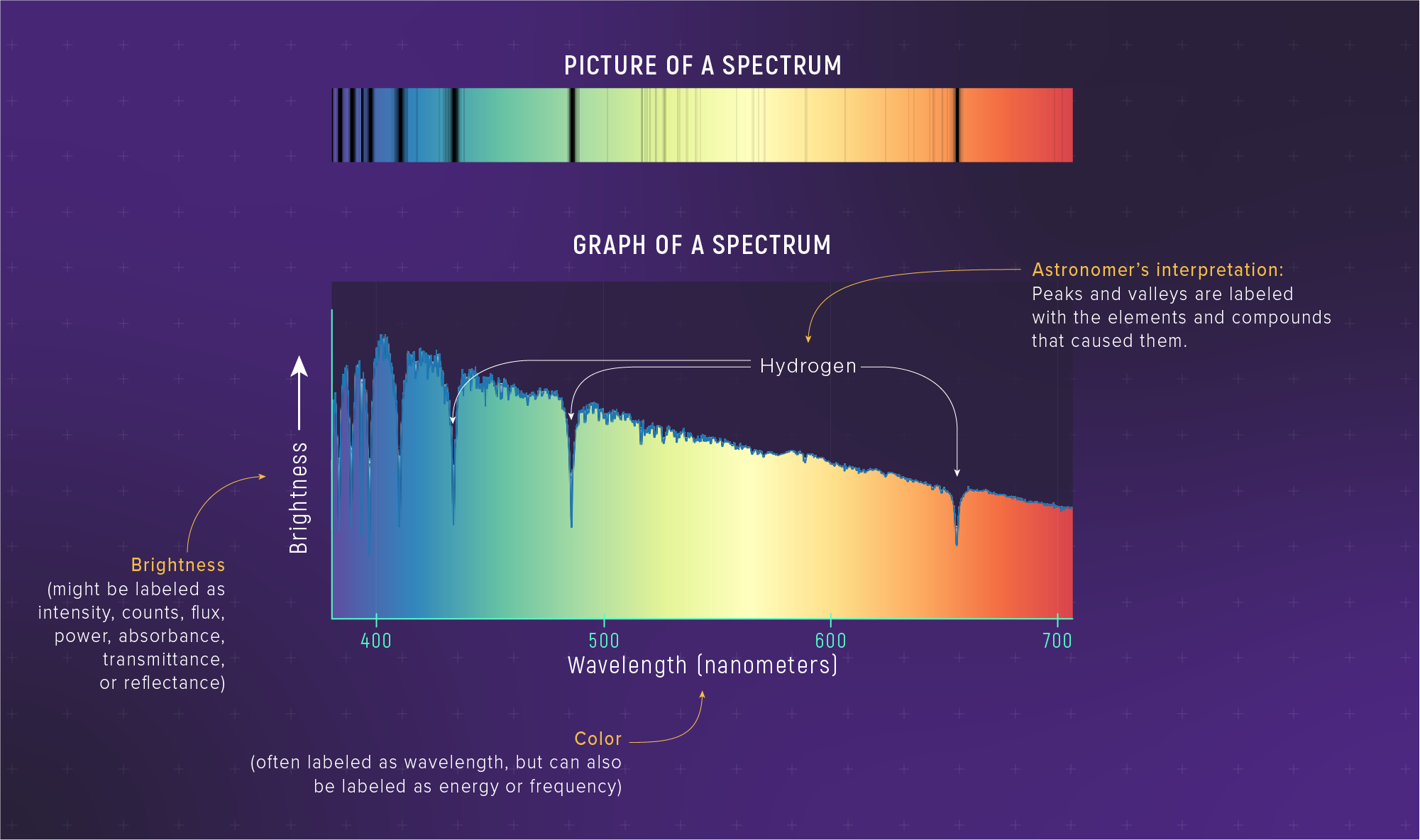
A Spectrum Is a Measurement

A spectrum is:

brightness as a function of wavelength

That’s more informative than a single “brightness number”.

Credit: JWST/STScI

Say the phrase “brightness vs wavelength” out loud. This is the object we’ll interpret all semester.

The Spectrum Reveals Different Physics

Credit: JWST/STScI

Call-and-response: “What does radio see?” “What does X-ray see?” Goal: internalize that wavelength choice is a physics choice.

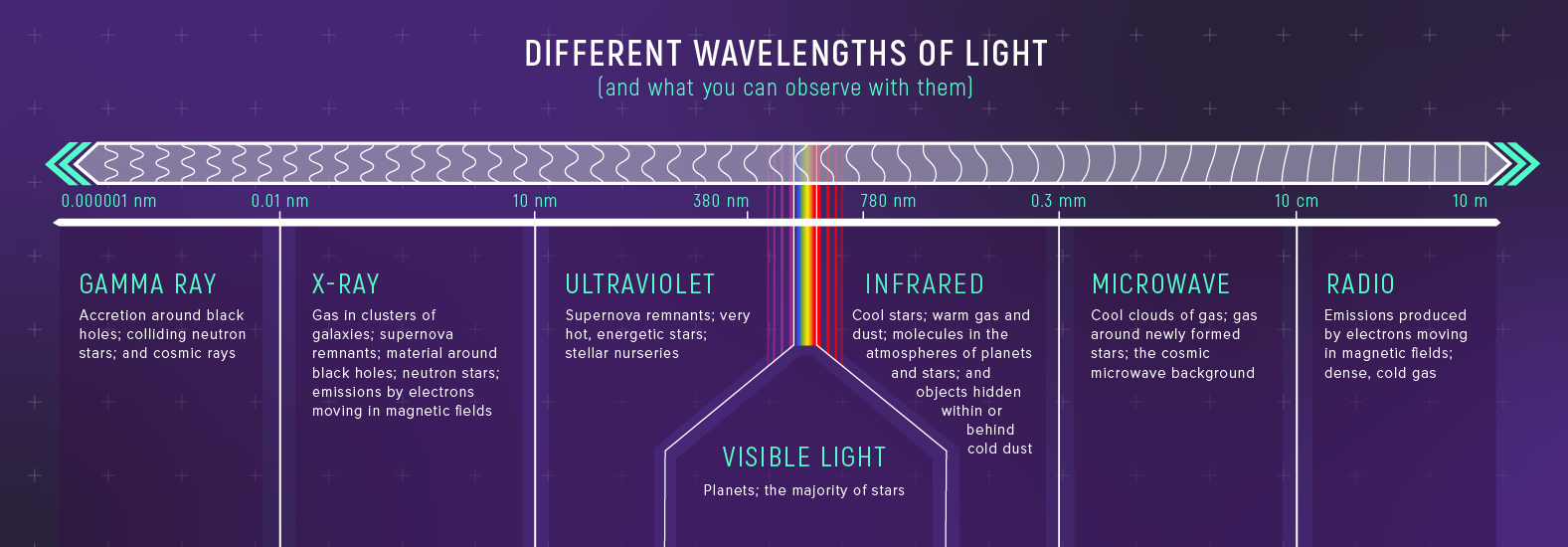
Same Universe — Different Physics

Credit: JWST/STScI

Different wavelengths highlight different components (stars, dust, gas).

Key line: the object didn’t change — the information channel did.

🧠 Think–Pair–Share

30–60 s

Which wavelength band is best for seeing into dusty star-forming regions?

• Visible
• Ultraviolet
• Infrared

Answer: Infrared — longer wavelengths pass through dust more easily.

Answer: infrared (dust is more transparent at longer wavelengths). Common misconception: “UV is more powerful so it sees through.”

Part 2: Photons and Energy

Light is also made of particles.

Photon Energy

\[ E = h\nu = hc\lambda^{-1} \tag{3}\]

Credit: JWST/STScI

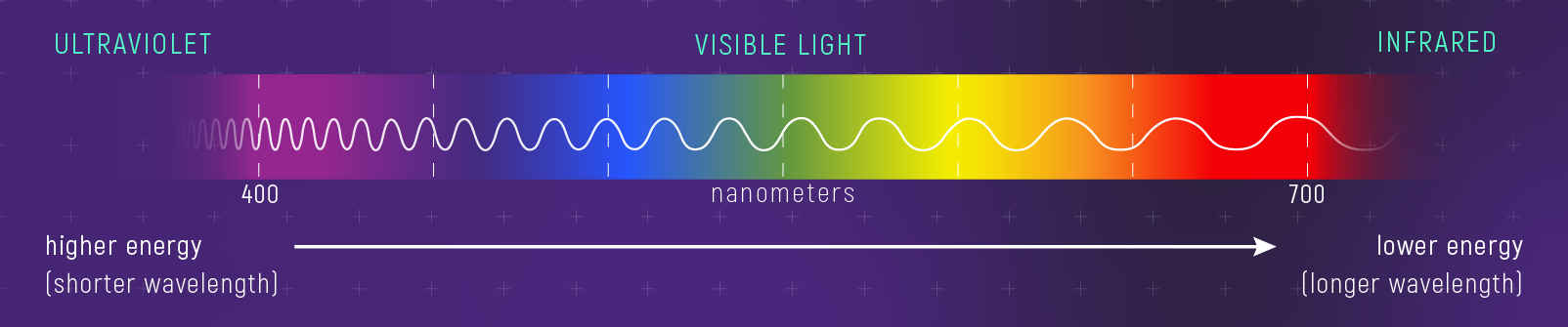
What this equation is saying:

• Direct: \(E \propto \nu\)
• Inverse: \(E \propto \lambda^{-1}\) (same as \(E \propto 1/\lambda\))

• shorter \(\lambda\) → larger \(E\)
• longer \(\lambda\) → smaller \(E\)

Here \(h\) is Planck’s constant (\(6.63\times10^{-27}\ \mathrm{erg\cdot s}\)).

Units check: (erg·s)·(s\(^{-1}\)) = erg.

Do not linger on constants. The point is scaling: \(E \propto \lambda^{-1}\).

Wave–Particle Duality

Optional but Helpful

Sometimes light behaves like a wave.

Sometimes it behaves like particles (photons).

Which model is useful depends on what you measure.

Credit: OpenStax

Keep this to ~60–90 seconds max. Goal: prevent “so the wave stuff was wrong?” No — different models, different experiments.

Spoiler Alert

For Later: Matter Waves

It’s not just light.

• particles also have wave behavior
• the “matter wavelength” gets shorter when momentum gets bigger
• \(p\) is momentum (in CGS: \(\mathrm{g\cdot cm/s}\))
• \(h\) is Planck’s constant (\(6.63\times10^{-27}\ \mathrm{erg\cdot s}\))

Teaser: \(\lambda = \frac{h}{p}\) (we’ll use this when we talk about stars in Module 2). This is a quantum-mechanics result linked to the Heisenberg uncertainty principle.

Do not explain quantum mechanics today. This is a trailer, not the movie.

🧠 Predict: Which Photon Is More Energetic?

Which photon has higher energy?

• 400 nm (blue)
• 800 nm (red / near-IR)
• same energy
• can’t tell without the telescope diameter

Quick reinforcement: shorter wavelength → higher energy. Answer: 400 nm (blue).

🧠 Predict: Scaling

If wavelength is cut in half, photon energy…

• is cut in half
• doubles
• quadruples
• stays the same

Answer: doubles.

Why Astronomers Care About Photon Energy

High-energy photons (UV/X-ray/gamma) can:

• ionize atoms
• heat million-degree plasma
• reveal extreme environments (accretion, explosions)

Low-energy photons (IR/radio) can:

• pass through dust
• trace cold gas and molecules

Keep qualitative. The takeaway is “different wavelengths → different interactions.”

Part 3: How Light Interacts with Matter

Light carries information because matter “filters” it.

Five Outcomes Plus Scattering

Credit: JWST/STScI

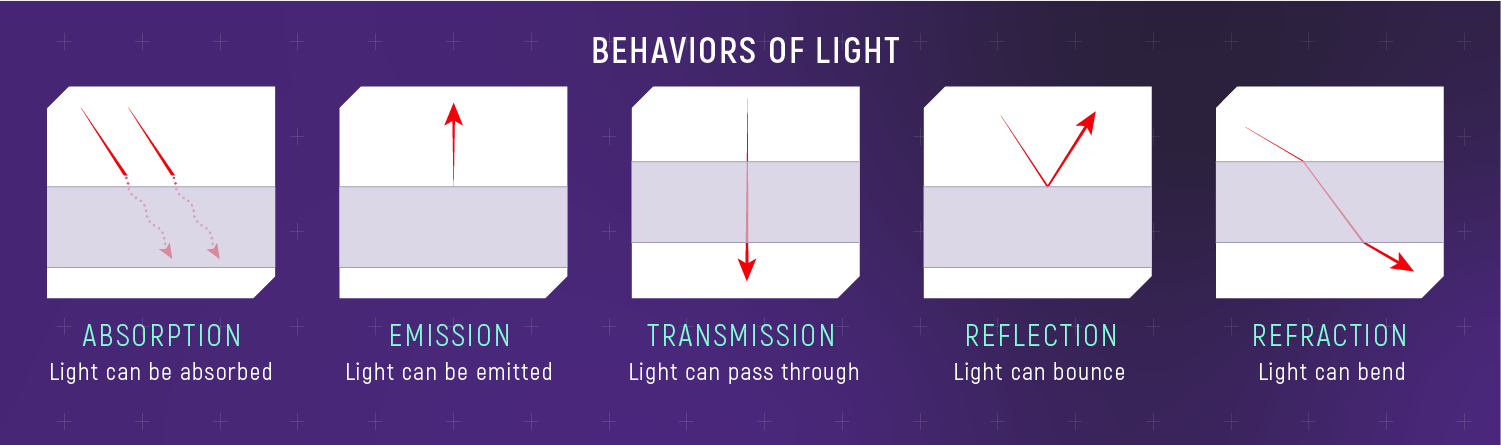
When light hits matter, it can be:

• transmitted
• absorbed
• emitted

• reflected / refracted
• scattered

Key move: these are not vocabulary words — they are “information pathways.”

Absorption and Emission

Tiny Preview

Absorption/emission are how light becomes a chemical fingerprint.

Next class: spectral lines tell us what a star is made of.

Keep this as a 20-second bridge so Day 2 feels inevitable.

Refraction and Dispersion

Preview

In glass, different wavelengths bend by different amounts.

That’s why prisms “spread out” white light.

Credit: JWST/STScI

If you want a micro-prompt: “Which bends more in the figure — red or blue?”

Scattering: Why the Sky Is Blue

For very small particles (like air molecules):

\[\text{scattering} \propto \lambda^{-4}\]

Shorter wavelength scatters much more.

Valid when particle size \(\ll \lambda\) (molecules).

Credit: NotebookLM

Don’t derive. Emphasize steep power: halve λ → 16× more scattering.

🧠 Predict: How Steep Is \(\lambda^{-4}\)?

If wavelength is cut in half, Rayleigh scattering becomes…

• 2× stronger
• 4× stronger
• 16× stronger
• 1/16 as strong

This is the “power-law intuition” skill: small wavelength changes can matter a lot. Answer: 16× stronger.

🧠 Predict: Rayleigh

On a planet with a similar atmosphere, which light scatters more?

• Blue (shorter wavelength)
• Red (longer wavelength)
• They scatter equally
• Only infrared scatters

Answer: Blue (shorter wavelength).

The Atmosphere Is a Filter

Earth’s atmosphere is not transparent everywhere.

• Optical window (good)
• Radio window (good)
• Some infrared gets through in atmospheric windows, but many bands are absorbed by molecules (H\(_2\)O, CO\(_2\), CH\(_4\), O\(_3\)).
• Most UV/X-ray/gamma blocked

Credit: NASA

This motivates space telescopes. Tie back to “observables are limited by physics and instruments.”

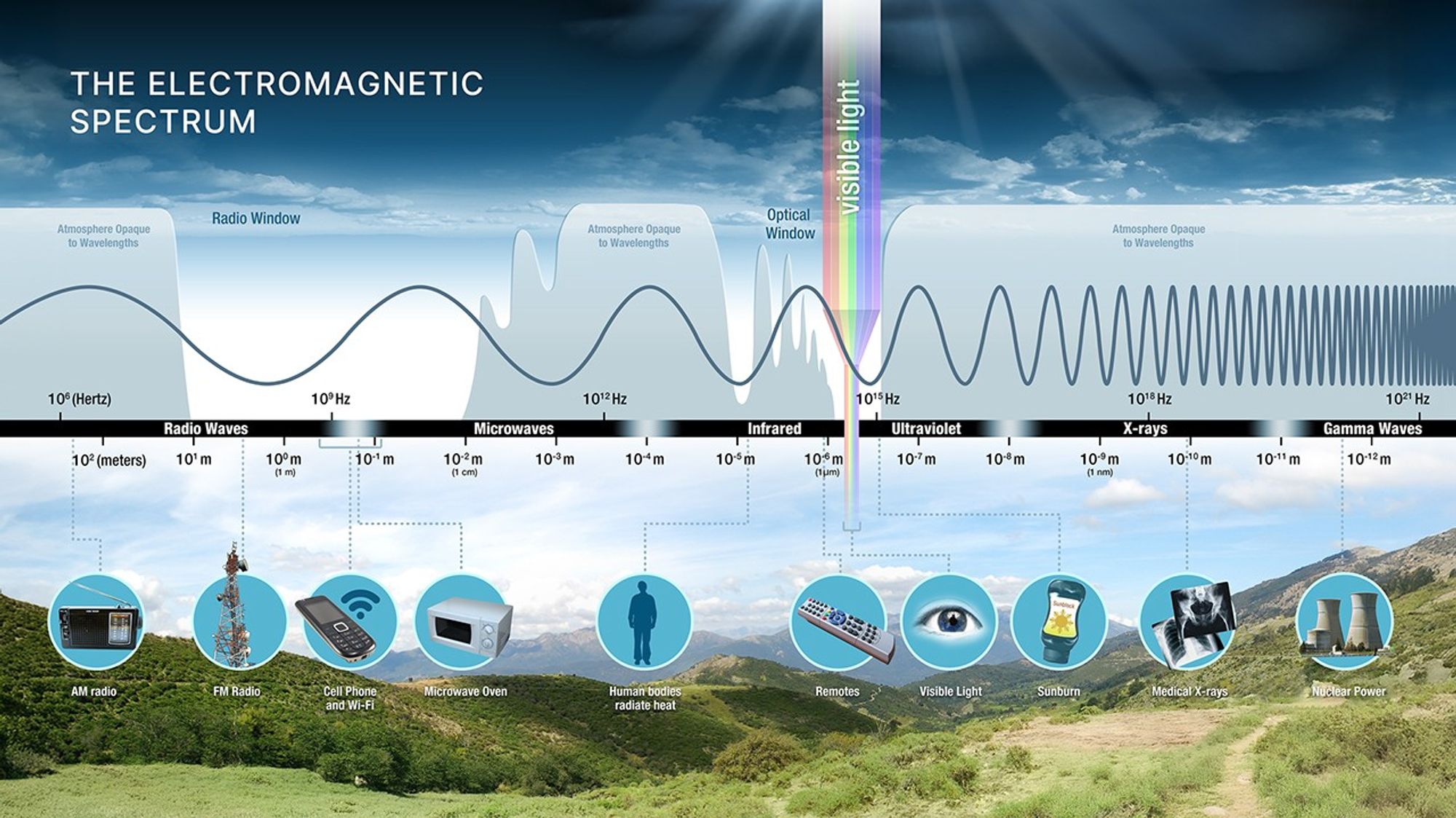
Opacity Preview: “How Far Light Gets”

Matter can be transparent or opaque depending on wavelength.

• dust blocks visible more than infrared
• Earth’s atmosphere blocks most UV/X-ray

Flag the word “opacity” as something we’ll use later, but don’t define optical depth yet.

Part 4: Thermal Radiation (Blackbodies)

Color encodes temperature.

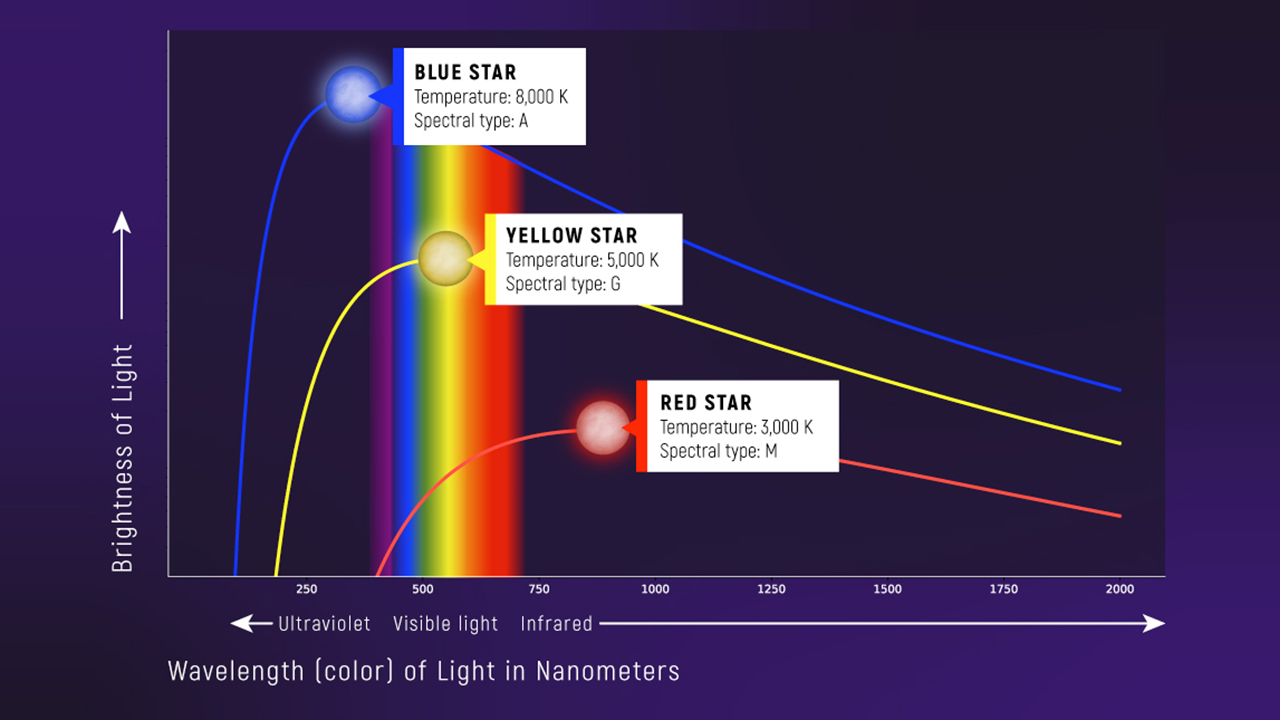
The Blackbody Idea

A blackbody is an ideal thermal emitter:

• spectrum shape depends mainly on temperature
• hotter objects emit more light and peak at shorter wavelength

Two-part misconception target: (1) “Hotter → bluer” (2) “Hotter → brighter overall.”

Why “Black”body?

An ideal blackbody:

• absorbs all wavelengths well (“black”)
• therefore emits thermal radiation efficiently

One sentence: good absorber ↔︎ good emitter (Kirchhoff’s law, qualitative).

Why Stars Are Approximately Blackbodies

Credit: JWST/STScI

Stars have a dense “surface” (the photosphere) where:

• photons interact many times with matter
• the radiation field becomes close to thermal

But atmospheres add spectral lines — next class we explain why.

Students may feel: “but stars aren’t perfect blackbodies.” Correct — this is a useful starting model. Module 2 (stellar structure + opacity) will make the approximation feel natural.

Two Things Change When \(T\) Changes

Credit: JWST/STScI

When temperature increases:

1. the peak shifts to shorter wavelength (Wien)
2. the total emitted light increases (area under the curve)

Preview for later: Stefan–Boltzmann. Don’t drop the equation yet — keep it conceptual.

The Key Pattern

Look, Don’t Memorize

Hotter → peak shifts left (bluer) and the whole curve gets taller.

Credit: JWST/STScI

Wien’s Law

Inference Tool #1

The peak wavelength of a thermal spectrum tells temperature:

\[ \lambda_{\text{peak}} = b T^{-1} \tag{4}\]

Wien constant: \(b \approx 0.2898\ \mathrm{cm\cdot K}\)

• \(\lambda_{\mathrm{peak}}\) shorter → \(T\) higher
• \(\lambda_{\mathrm{peak}}\) longer → \(T\) lower

Emphasize: inverse relationship (\(T^{-1}\)).

Units Check

Wien’s Law

If \(\lambda_{\mathrm{peak}} = bT^{-1}\), then \(b\) must have units of:

\[[\text{length}]\cdot[\text{temperature}]\]

Quick “units as logic” reinforcement.

🧠 Predict: Scaling

If temperature doubles, the peak wavelength becomes…

• half as large
• twice as large
• unchanged
• four times larger

Answer: half as large.

🧠 Predict: No Numbers

A star with a shorter peak wavelength is…

• hotter
• cooler
• the same temperature
• older

Answer: hotter.

Worked Example: The Sun

Fast

Take \(\lambda_{\mathrm{peak}} \approx 500\ \mathrm{nm} = 5\times10^{-5}\ \mathrm{cm}\).

. . .

Use \(b \approx 0.29\ \mathrm{cm\cdot K}\):

\[T \approx 0.29\cdot(5\times10^{-5})^{-1} \approx 5.8\times10^{3}\ \mathrm{K}\]

Round aggressively. This is “order-of-magnitude plus one digit”, not a precision measurement.

Stop & Solve: Compare Two Peaks

Star A peaks at \(500\ \mathrm{nm}\).

Star B peaks at \(1000\ \mathrm{nm}\).

How do their temperatures compare?

Give 30–45 s. Expect “inverse” reasoning.

Stop & Solve — Solution

Because \(\lambda_{\mathrm{peak}} \propto T^{-1}\):

\[\frac{T_B}{T_A} = \frac{\lambda_A}{\lambda_B} = \frac{500\ \mathrm{nm}}{1000\ \mathrm{nm}} = \frac{1}{2}\]

Units cancel in the ratio, so the temperature ratio is dimensionless.

Star B is half the temperature of Star A.

Worked Example: A Cool Star

Fast

Suppose \(T \approx 3500\ \mathrm{K}\) (a cool red supergiant).

\[\lambda_{\mathrm{peak}} \approx 0.29\cdot(3500)^{-1}\ \mathrm{cm}\approx 8.3\times10^{-5}\ \mathrm{cm}\approx 830\ \mathrm{nm}\]

That’s just beyond visible red → near infrared.

This is intentionally “fast math.” The point is: cooler objects peak in IR, not that students memorize Betelgeuse.

“Big Star” Context

Optional Wow

Betelgeuse is an example.

Credit: ESO/L. Calçada

One-sentence tie-in: cool objects can still be luminous if they have huge surface area (preview: Stefan–Boltzmann + radius).

A Common Misconception

“If a star peaks in the UV, it emits only UV.”

No — a hot blackbody emits across many wavelengths.

Misconception alert: Students often think “peak wavelength” = “only wavelength emitted.” Use the blackbody figure: hot curve is above cool curve even in the red. Emphasize the breadth of the Planck curve — color is about the ratio of blue to red light, not just where the peak sits.

Next Class

Day 2: Continuum + Lines

Blackbody is the starting model.

Next class we add:

• absorption lines → composition
• (later) Doppler shifts → motion

Credit: JWST/STScI

Synthesis

Day 1

Today we built the chain:

• Measure: spectrum (intensity vs wavelength)
• Model: blackbody thermal emission
• Infer: temperature (via Wien’s law)

Next class: the fine structure (spectral lines) → composition.

Demo Time

If Time: EM Spectrum

Demo: em-spectrum

Prompt: Where is “visible” on a log scale? What changes fastest: \(\lambda\), \(\nu\), or \(E\)?

Local path (instructor): /Users/anna/Teaching/astr101-sp26/demos/em-spectrum/ Suggested flow (3–5 min): 1) Start at visible (550 nm), then jump to radio and gamma. 2) Ask: “How many orders of magnitude did we move?” 3) Reinforce: longer λ → lower ν → lower E. If short on time: skip and remind students demos are posted.

Demo Time

If Time: Blackbody Radiation

Demo: blackbody-radiation

Prompt: As \(T\) increases, what happens to (1) peak wavelength and (2) total emitted light?

Local path (instructor): /Users/anna/Teaching/astr101-sp26/demos/blackbody-radiation/ Suggested flow (3–6 min): 1) Start at 3000 K vs 8000 K (comparison mode if available). 2) Ask for two predictions before moving the slider: “which way does the peak move?” “what happens to area under the curve?” 3) Tie back to Wien (peak) and preview Stefan–Boltzmann (area). If short on time: do 60 seconds — just show the peak shifting.

Exit Ticket

30 seconds

Write one sentence:

“A spectrum is useful because…”

Collect 2–3 aloud. Listen for “we can infer temperature/composition from wavelength-dependent behavior.”

Study Snapshot

Write This Down

• \(c=\lambda\nu\) (wave relation)
• \(E=hc\lambda^{-1}\) (shorter \(\lambda\) → higher energy)
• \(\lambda_{\rm peak}=bT^{-1}\) (shorter peak → hotter)
• \(E \propto \nu\) and \(E \propto \lambda^{-1}\)
• \(\lambda_{\rm peak} \propto T^{-1}\)

This is the “exam-memory” slide. Keep students focused on interpretations.